题目内容
为了庆祝“元旦“,学校买了两挂同样长的鞭炮,在东西校区同时点燃,结果东校区那一挂每分钟缩短4m西校区那一挂每分钟缩短3m,两分钟后,其中一挂的长度是另一挂的1.5倍.
(1)求每挂鞭炮原来的长度;
(2)有人说:“如果东校区那一挂加长3m(特性和原来一样,同时点燃,两挂鞭炮将同时炸完.“你同意这种说法吗?为什么?
(3)如果让你去放这两挂鞭炮,请设计出一种方案,使两挂鞭炮同时点燃且同时炸完,简要说明理由.
(1)求每挂鞭炮原来的长度;
(2)有人说:“如果东校区那一挂加长3m(特性和原来一样,同时点燃,两挂鞭炮将同时炸完.“你同意这种说法吗?为什么?
(3)如果让你去放这两挂鞭炮,请设计出一种方案,使两挂鞭炮同时点燃且同时炸完,简要说明理由.
考点:一元一次方程的应用
专题:应用题
分析:(1)设每挂鞭炮原来的长度为xm,东校区那一挂每分钟放4m,西校区那一挂每分钟放3m,利用两分钟后,其中一挂的长度是另一挂的1.5倍列方程得x-2×3=1.5(x-2×4),然后解方程;
(2)算出东校区那一挂炸完所用时间和西校区那一挂炸完所用时间,根据时间不相等进行判断;
(3)把东校区那一挂加长4m,则东校区那一挂炸完所用时间=(12+4)÷4=4,正好与西校区那一挂炸完所用时间相等.
(2)算出东校区那一挂炸完所用时间和西校区那一挂炸完所用时间,根据时间不相等进行判断;
(3)把东校区那一挂加长4m,则东校区那一挂炸完所用时间=(12+4)÷4=4,正好与西校区那一挂炸完所用时间相等.
解答:解:(1)设每挂鞭炮原来的长度为xm,
根据题意得x-2×3=1.5(x-2×4),
解得x=12.
答:每挂鞭炮原来的长度为12m;
(2)东校区那一挂炸完所用时间=(12+3)÷4=
,
而西校区那一挂炸完所用时间=12÷3=4,
所以不同意这种说法;
(3)东校区那一挂加长4m(特性和原来一样,同时点燃,两挂鞭炮将同时炸完.
东校区那一挂炸完所用时间=(12+4)÷4=4,
而西校区那一挂炸完所用时间=4,
所以两挂鞭炮同时点燃且同时炸完.
根据题意得x-2×3=1.5(x-2×4),
解得x=12.
答:每挂鞭炮原来的长度为12m;
(2)东校区那一挂炸完所用时间=(12+3)÷4=
| 15 |
| 4 |
而西校区那一挂炸完所用时间=12÷3=4,
所以不同意这种说法;
(3)东校区那一挂加长4m(特性和原来一样,同时点燃,两挂鞭炮将同时炸完.
东校区那一挂炸完所用时间=(12+4)÷4=4,
而西校区那一挂炸完所用时间=4,
所以两挂鞭炮同时点燃且同时炸完.
点评:本题考查了一元一次方程的应用:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.

练习册系列答案
相关题目
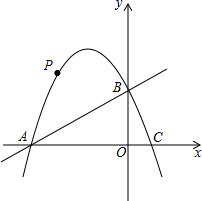 在平面直角坐标系中,直线y=x+4与x、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并与x轴交于另一点C(点C在点A的右侧),点P是抛物线上的一个动点.
在平面直角坐标系中,直线y=x+4与x、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并与x轴交于另一点C(点C在点A的右侧),点P是抛物线上的一个动点.