Question

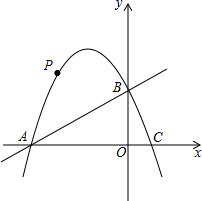在平面直角坐标系中，直线y=x+4与x、y轴分别交于A、B两点，抛物线y=-x²+bx+c经过A、B两点，并与x轴交于另一点C（点C在点A的右侧），点P是抛物线上的一个动点．
（1）求抛物线解析式及点C；
（2）若点P在第二象限内，过点P作PD⊥x轴于点D，交AB于点E，当点P运动到什么位置时，PE最长是多少？

Answer 1

考点：二次函数综合题

专题：

分析：（1）先求出点A、B的坐标，然后代入二次函数解析式，求出b、c的值，以及点C的坐标；
（2）设P点横坐标为m，求出P点纵坐标以及点E的纵坐标，求出PE的长度，利用二次函数求极值的方法求出PE长度的最大值．

解答：解：（1）∵直线y=x+4与x、y轴分别交于A、B两点，
∴A（-4，0），B（0，4），
将点A、B坐标代入解析式得：

-16-4b+c=0 c=4

，
解得：

b=-3 c=4

，
则二次函数的解析式为：y=-x²-3x+4，
令-x²-3x+4=0，
解得：x₁=4，x₂=1，
点C坐标为（1，0）；

（2）设P点横坐标为m，
则纵坐标为-m²-3m+4，
E点纵坐标为m+4，
则PE=-m²-3m+4-（m+4）=-m²-3m+4-m-4=-m²-4m=-（m+2）²+4，
当m=-2时，PE有最大值4，
此时点P纵坐标为6，
故当点P运动到（-2，6）时，PE最长为4．

点评：本题综合考查了二次函数的图象与性质、待定系数法、一次函数、一元二次方程的解法及判别式、等腰三角形以及勾股定理等方面知识，涉及考点较多，难度较大．