题目内容
已知：如图，在△ABC中，AB=AC，∠ABC和∠ACB的平分线交于点P．求证：PB=PC．
考点：等腰三角形的判定与性质
专题：证明题
分析：由AB=AC得出∠ABC=∠ACB，再利用角平分线的意义得出∠PBC=∠PCB，求得结论．
解答：证明：∵AB=AC，
∴∠ABC=∠ACB（等边对等角），
又∵PB、PC是角平分线，
∴∠PBC=∠PCB（等式的性质），
∴PB=PC（等角对等边）．
∴∠ABC=∠ACB（等边对等角），
又∵PB、PC是角平分线，
∴∠PBC=∠PCB（等式的性质），
∴PB=PC（等角对等边）．
点评：此题考查等腰三角形的性质与判定，角平分线的意义，以及等量代换求得结论．
练习册系列答案
阅读快车系列答案
相关题目
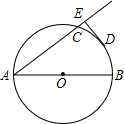如图，AB、AC分别是⊙O的直径和弦，D为
如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF．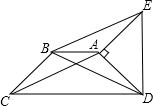
如图，在等腰梯形ABCD中，已知AB∥CD，AD=BC，∠ADC=45°，将腰AD绕A点逆时针旋转90°，得到AE，连接BE、DE、AC、BD．求证：四边形ACBE是平行四边形．
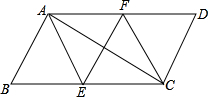如图，?ABCD中，AE、CF分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是
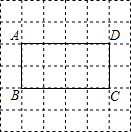如图，所有小正方形的边长都为1，长方形的顶点都在格点上．请按要求解答：