题目内容
16.如图,在矩形纸片ABCD中,AB=10,AD=8;将矩形纸片沿折痕DF折叠,使点C叠在AB边上的点E处.(1)求证:△ADE∽△BEF;
(2)求BF的长;
(3)问在边DC上是否存在一点P,使得△FCP与△BEF相似?若存在请求出此时CP的长;若不存在请说明理由.

分析 (1)根据矩形的性质,可得∠A=∠B=∠C,根据直角三角形的性质,可得∠1与∠3的关系,根据折叠的性质,可得∠DEF=∠C,根据角的和差,可得∠1与∠2的关系,根据余角的性质,可得∠2与∠3的关系,根据相似三角形的判定,可得答案;
(2)根据折叠的性质,可得DE与BC的关系,CF与BE的关系,根据勾股定理,可得AE的长,根据相似三角形的性质,可得关于BF的方程,根据解方程,可得答案;
(3)根据相似三角形的性质,可得关于CP的方程,根据解方程,可得答案.
解答 (1)证明:如图1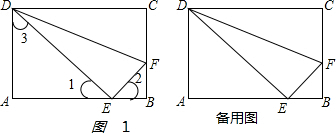 ,
,
∵ABCD是矩形,
∴∠A=∠B=∠C=90°,
∴∠1+∠3=90°.
∵折叠,
∴∠DEF=∠C═90°,
∴∠1+∠2=90°,
∴∠2=∠3,
∴△ADE∽△BEF;
(2)∵折叠,
∴DE=DC=10,CF=EF.
在Rt△ADE中,AE=$\sqrt{{{10}^2}-{8^2}}$=6,
∴BE=10-6=4.
∵△ADE∽△BEF,
∴$\frac{AE}{BF}$=$\frac{AD}{BE}$,即$\frac{6}{BF}$=$\frac{8}{4}$.
解得BF=3;
(3)如图2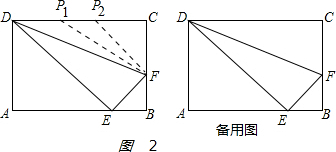 ,
,
∵∠B=∠C,BE=4,BF=3,CF=BC-BF=5.
①当△CFP∽△BEF时,$\frac{CF}{BE}$=$\frac{CP}{BF}$,即$\frac{5}{4}$=$\frac{CP}{3}$,
解得CP=$\frac{15}{4}$;
②当△CFP∽△②BEF时$\frac{CP}{BE}$=$\frac{CF}{BF}$,即$\frac{CP}{4}$=$\frac{5}{3}$,
解得CP=$\frac{20}{3}$;
综上所述,存在点P,使△FCP与△BEF相似,
此时,CP=$\frac{15}{4}$或$\frac{20}{3}$.
点评 本题考查了相似形综合题,利用了矩形的性质,直角三角形的性质,相似三角形的判定,利用余角的性质得出∠2=∠3是解题关键;利用了勾股定理,相似三角形的性质;利用相似三角形的性质得出关于CP的方程是解题关键,要分类讨论,以防遗漏.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案 如图是用两个边长不等的正方形连在一起的“L”形纸片,
如图是用两个边长不等的正方形连在一起的“L”形纸片,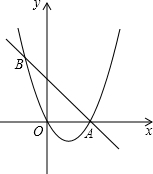 如图,二次函数y=x2+bx+c图象经过原点和点A(2,0),直线AB与抛物线交于点B,且∠BAO=45°.
如图,二次函数y=x2+bx+c图象经过原点和点A(2,0),直线AB与抛物线交于点B,且∠BAO=45°.