题目内容
11.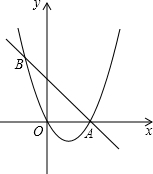 如图,二次函数y=x2+bx+c图象经过原点和点A(2,0),直线AB与抛物线交于点B,且∠BAO=45°.
如图,二次函数y=x2+bx+c图象经过原点和点A(2,0),直线AB与抛物线交于点B,且∠BAO=45°.(1)求二次函数解析式及其顶点C的坐标;
(2)在直线AB上是否存在点D,使得△BCD为直角三角形?若存在,求出点D的坐标;若不存在,说明理由.
分析 (1)将点A和点O的坐标代入抛物线的解析式可求得b=-2,c=0,从而得到抛物线的解析式,由抛物线的对称性可知点C的横坐标为1,将x=1代入抛物线的解析式可求得y=-1,故此可求得点C的坐标;
(2)由∠BAO=45°可知直线AB的一次项系数为-1,从而可求得直线AB的解析式为y=-x+2.如图1所示:当∠ADC=90°时.依据相互垂直的两直线的一次项系数之积等于-1可求得直线CD的解析式为y=x-2,将y=-x+2与y=x-2联立可求得点D的坐标为(2,0);如图2所示:当∠BCD=90°时.将y=-x+2与y=x2-2x联立得求得点B的坐标为(-1,3),然后依据待定系数法求得直线BC的解析式为直线BC的解析式为y=-2x+1,依据相互垂直的两直线的一次项系数之积等于-1可求得直线CD的解析式为y=$\frac{1}{2}x-\frac{3}{2}$,将y=-x+2与y=$\frac{1}{2}x-\frac{3}{2}$联立可求得点Q的坐标为($\frac{7}{3}$,-$\frac{1}{3}$).
解答 解:(1)将(0,0)、(2,0)代入函数的解析式得:$\left\{\begin{array}{l}{4+2b+c=0}\\{c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-2}\\{c=0}\end{array}\right.$.
二次函数的解析式为y=x2-2x.
∵点(0,0)与(2,0)关于x=1对称,
∴抛物线的对称轴为x=1.
将x=1代入得:y=-1.
∴点C的坐标为(1,-1).
(2)∵∠BAO=45°,
∴直线AB的一次项系数为-1.
设直线AB的解析式为y=-x+b,将(2,0)代入得:-2+b=0,
解得:b=2.
∴直线AB的解析式为y=-x+2.
如图1所示:当∠ADC=90°时.
∵∠ADC=90°,
∴CD⊥AB.
∴直线CD与直线AB的一次项系数的乘以为-1.
∴直线CD的一次项系数为1.
设直线CD的解析式为y=x+b.
∵将C(1,-1)代入得:1+b=-1.解得:b=-2,
∴直线CD的解析式为y=x-2.
将y=-x+2与y=x-2联立得:$\left\{\begin{array}{l}{y=-x+2}\\{y=x-2}\end{array}\right.$.
解得:x=2,y=0.
∴点D的坐标为(2,0).
如图2所示:当∠BCD=90°时.
∵将y=-x+2与y=x2-2x联立得:$\left\{\begin{array}{l}{y=-x+2}\\{y={x}^{2}-2x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$,
∴点B的坐标为(-1,3).
设直线BC的解析式为y=kx+b,将(-1,3)、(1,-1)代入得:$\left\{\begin{array}{l}{-k+b=3}\\{k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=1}\end{array}\right.$.
∴直线BC的解析式为y=-2x+1.
∵CD⊥BC,
∴直线CD的一次项系数为$\frac{1}{2}$.
设直线CD的解析式为y=$\frac{1}{2}x$+c,将点C的坐标代入得:$\frac{1}{2}×1+c$=-1.
解得:c=$-\frac{3}{2}$.
∴直线CD的解析式为y=$\frac{1}{2}x-\frac{3}{2}$.
将y=-x+2与y=$\frac{1}{2}x-\frac{3}{2}$联立得:$\left\{\begin{array}{l}{y=-x+2}\\{y=\frac{1}{2}x-\frac{3}{2}}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{x=\frac{7}{3}}\\{y=-\frac{1}{3}}\end{array}\right.$.
∴点Q的坐标为($\frac{7}{3}$,-$\frac{1}{3}$).
由图形可知∠CBD=90°的情况不存在.
综上所述,点Q的坐标为(2,0)或($\frac{7}{3}$,$-\frac{1}{3}$).
点评 本题主要考查的是二次函数与一次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二函数的解析式、二元二次方程组和二元一次方程组的应用,明确相互垂直的两直线的一次项系数之积等于-1是解题的关键.

| A. | -9 | B. | -3 | C. | 3 | D. | 9 |
| A. | (a3)2÷a5=a10 | B. | (a4)2÷a4=a2 | ||
| C. | (-5a2b3)•(-2a)=10a3b3 | D. | (-a3b)3÷$\frac{1}{2}{a^2}{b^2}=-2{a^4}$b |
 如图所示,要测量河两岸A,B间的距离,可用什么方法?并说明这样做的合理性.
如图所示,要测量河两岸A,B间的距离,可用什么方法?并说明这样做的合理性. 如图,已知A(-2,3)、B(-5,0)、C(-1,0).
如图,已知A(-2,3)、B(-5,0)、C(-1,0). 已知△ADC≌△CEB,写出两个全等三角形的对应边及对应角.
已知△ADC≌△CEB,写出两个全等三角形的对应边及对应角.