题目内容
6.已知m是方程x2-2017x+1=0的一个根,则代数式m2-2018m+$\frac{{m}^{2}+1}{2017}$+3的值是2.分析 根据一元二次方程根的定义得到m2=2017m-1,再利用整体代入的方法得到原式=2017m-1-2018m+$\frac{2017m-1+1}{2017}$+3,然后合并即可.
解答 解:∵m是方程x2-2017x+1=0的一个根,
∴m2-2017m+1=0,
∴m2=2017m-1,
∴原式=2017m-1-2018m+$\frac{2017m-1+1}{2017}$+3
=-1-m+m+3
=2.
故答案为2.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
18.快递公司2014年的快递业务量为2亿件,受益于经济的快速增长及电子商务发展等多重因素,快递业务迅猛发展,2016年的快递业务量达到3.92亿件.若设该地区这两年快递业务量的年平均增长率为x,则下列方程正确的是( )
| A. | 2(1-x)2=3.92 | B. | 3.92(1-x)2=2 | C. | 2(1+x)2=3.92 | D. | 3.92(1+x)2=2 |
15.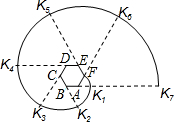 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )
 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )| A. | $\frac{2016π}{2}$ | B. | $\frac{2016π}{3}$ | C. | $\frac{2016π}{4}$ | D. | $\frac{2016π}{6}$. |
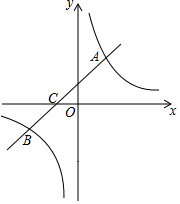 如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).
如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).