题目内容
9.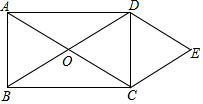 如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为10$\sqrt{3}$,求AC的长.
分析 (1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形CODE是菱形,
(2)根据菱形OCED的面积=2△OCD的面积=△ACD的面积=$\frac{1}{2}$AD•CD=10$\sqrt{3}$,证出AC=2CD,AD=$\sqrt{3}$CD,得出$\frac{1}{2}$×$\sqrt{3}$CD•CD=10$\sqrt{3}$,求出CD,即可得出答案.
解答 (1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,∠ADC=∠ABC=∠BAD=90°,
∴OD=OC,
∴四边形OCED是菱形;
(2)解:∵四边形OCED是菱形,
∴菱形OCED的面积=2△OCD的面积=△ACD的面积=$\frac{1}{2}$AD•CD=10$\sqrt{3}$,
∵∠ACB=30°,
∴∠BAC=60°,
∴∠DAC=30°,
∴AC=2CD,AD=$\sqrt{3}$CD,
∴$\frac{1}{2}$×$\sqrt{3}$CD•CD=10$\sqrt{3}$,
解得:CD=2$\sqrt{5}$,
∴AC=2CD=4$\sqrt{5}$.
点评 此题考查了矩形的性质、菱形的判定与性质、直角三角形的性质、勾股定理等知识,熟练掌握菱形的判定方法是解题的关键,记住矩形的对角线把矩形分成面积相等的4个三角形,属于中考常考题型.

练习册系列答案
相关题目
18.快递公司2014年的快递业务量为2亿件,受益于经济的快速增长及电子商务发展等多重因素,快递业务迅猛发展,2016年的快递业务量达到3.92亿件.若设该地区这两年快递业务量的年平均增长率为x,则下列方程正确的是( )
| A. | 2(1-x)2=3.92 | B. | 3.92(1-x)2=2 | C. | 2(1+x)2=3.92 | D. | 3.92(1+x)2=2 |
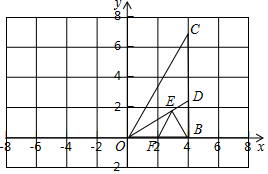 如图,Rt△OBC中,OB=4,∠BOC=60°,∠BOC的平分线交BC于D,E、F分别是OD、OB上的动点,BE+EF取到最小值时,E点坐标为(2,$\frac{2\sqrt{3}}{3}$).
如图,Rt△OBC中,OB=4,∠BOC=60°,∠BOC的平分线交BC于D,E、F分别是OD、OB上的动点,BE+EF取到最小值时,E点坐标为(2,$\frac{2\sqrt{3}}{3}$).