题目内容
7.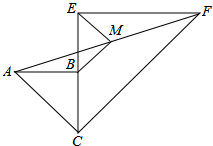 如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)求证:MB∥CF;
(2)若CB=a,CE=2a,求BM,ME的长.
分析 (1)如答图1所示,延长AB交CF于点D,证明BM为△ADF的中位线即可;
(2)先求出BE的长,再根据全等三角形对应边相等可得BM=DM,根据等腰三角形三线合一的性质可得EM⊥BD,求出△BEM是等腰直角三角形,根据等腰直角三角形的性质求解即可;
解答 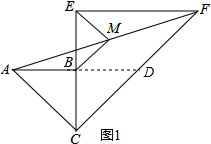 解:(1)如图1,延长AB交CF于点D,
解:(1)如图1,延长AB交CF于点D,
则易知△ABC与△BCD均为等腰直角三角形,
∴AB=BC=BD,
∴点B为线段AD的中点,
又∵点M为线段AF的中点,
∴BM为△ADF的中位线,
∴BM∥CF;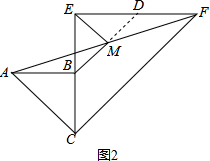
(2)如图2,
∵CB=a,CE=2a,
∴BE=CE-CB=2a-a=a,
∵△ABM≌△FDM,
∴BM=DM,
又∵△BED是等腰直角三角形,
∴△BEM是等腰直角三角形,
∴BM=ME=$\frac{\sqrt{2}}{2}$BE=$\frac{\sqrt{2}}{2}$a.
点评 本题考查了三角形中位线定理、全等三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出中位线、全等三角形和等腰直角三角形是解题的关键,也是本题的难点.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
18. 如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
 如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )
如图,AB∥EF∥CD,AD∥MN∥BC,则图中共有平行四边形( )| A. | 6个 | B. | 7个 | C. | 8个 | D. | 9个 |
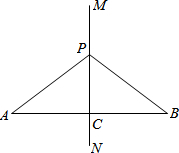 如图,直线MN⊥AB,垂足为C,且AC=BC,P是MN的任意一点.求证:PA=PB.
如图,直线MN⊥AB,垂足为C,且AC=BC,P是MN的任意一点.求证:PA=PB.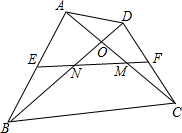 在四边形ABCD中,ACBD相交于O点,AC=BD,E、F分别是AB,CD的中点,连接EF分别交AC、BD于M、N,判断三角形MON的形状,并说明理由.
在四边形ABCD中,ACBD相交于O点,AC=BD,E、F分别是AB,CD的中点,连接EF分别交AC、BD于M、N,判断三角形MON的形状,并说明理由.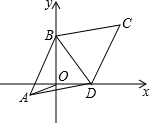 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.
如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是5$\sqrt{3}$-5.