题目内容
19.对于一切不小于2的自然数n,关于x的一元二次方程x2-(n+2)x-2n2=0的两个根记作an,bn(n≥2),则$\frac{1}{{({a_2}-2)({b_2}-2)}}$$+\frac{1}{{({a_3}-2)({b_3}-2)}}$+…$\frac{1}{({a}_{2012}-2)({b}_{2012}-2)}$=-$\frac{2011}{8052}$.分析 由根与系数的关系得an+bn=n+2,an•bn=-2n2,所以(an-2)(bn-2)=anbn-2(an+bn)+4=-2n2-2(n+2)+4=-2n(n+1),则$\frac{1}{({a}_{n}-2)({b}_{n}-2)}$=-$\frac{1}{2n(n+1)}$=-$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),然后代入即可求解.
解答 解:由根与系数的关系得an+bn=n+2,an•bn=-2n2,
所以(an-2)(bn-2)=anbn-2(an+bn)+4=-2n2-2(n+2)+4=-2n(n+1),
则$\frac{1}{({a}_{n}-2)({b}_{n}-2)}$=-$\frac{1}{2n(n+1)}$=-$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴$\frac{1}{{({a_2}-2)({b_2}-2)}}$$+\frac{1}{{({a_3}-2)({b_3}-2)}}$+…$\frac{1}{({a}_{2012}-2)({b}_{2012}-2)}$=-$\frac{1}{2}$[($\frac{1}{2}-\frac{1}{3}$)+($\frac{1}{3}+\frac{1}{4}$)+…+($\frac{1}{2012}-\frac{1}{2013}$)]=-$\frac{1}{2}$($\frac{1}{2}-\frac{1}{2013}$)=-$\frac{1}{2}$×$\frac{2011}{4026}$=-$\frac{2011}{8052}$.
故答案为:-$\frac{2011}{8052}$.
点评 本题考查了根与系数的关系,难度较大,关键是根据根与系数的关系求出一般形式再进行代入求值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 两个互补的角中必有一个是钝角 | |
| B. | 一个角的补角一定比这个角大 | |
| C. | 互补的两个角中至少有一个角大于或等于直角 | |
| D. | 相等的角一定互余 |
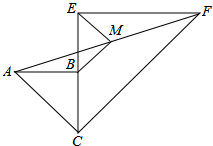 如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)求证:MB∥CF;
(2)若CB=a,CE=2a,求BM,ME的长.
| A. | y=(x-3)2-2 | B. | y=(x-1)2+4 | C. | y=(x-3)2+4 | D. | y=(x-2)2-2 |
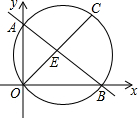 如图,直线y=-$\frac{3}{4}$x+6交x轴于点B,交y轴于点A,以AB为直径作圆,点C是$\widehat{AB}$的中点,连接OC交直径AB于点E,则OC的长为7$\sqrt{2}$.
如图,直线y=-$\frac{3}{4}$x+6交x轴于点B,交y轴于点A,以AB为直径作圆,点C是$\widehat{AB}$的中点,连接OC交直径AB于点E,则OC的长为7$\sqrt{2}$.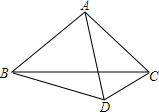 如图,△ABC是等边三角形,点D是△ABC外一点,试证明:DB+DC≥AD.
如图,△ABC是等边三角形,点D是△ABC外一点,试证明:DB+DC≥AD.