题目内容
12.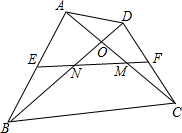 在四边形ABCD中,ACBD相交于O点,AC=BD,E、F分别是AB,CD的中点,连接EF分别交AC、BD于M、N,判断三角形MON的形状,并说明理由.
在四边形ABCD中,ACBD相交于O点,AC=BD,E、F分别是AB,CD的中点,连接EF分别交AC、BD于M、N,判断三角形MON的形状,并说明理由.
分析 取BC边的中点G,连接EG,FG.根据三角形中位线定理得到GE=GF,根据平行线的性质和等量代换得到∠OMN=∠ONM,根据等腰三角形的判定定理证明结论.
解答 解: 如图,取BC边的中点G,连接EG,FG.
如图,取BC边的中点G,连接EG,FG.
∵E、F分别是AB、CD的中点,
∴EG∥AC,EG=$\frac{1}{2}$AC,
同理:FG∥BD,FG=$\frac{1}{2}$BD,
∵AC=BD,
∴EG=FG,
∴∠GEF=∠GFE.
∵EG∥AC,
∴∠OMN=∠GEF.
同理,∠ONM=∠GFE.
∴∠OMN=∠ONM,
∴OM=ON.即△MON是等腰三角形.
点评 本题考查了三角形的中位线定理和等腰三角形的判定,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
20.下列说怯正确的是( )
| A. | 有一组对角是直角的四边形一定是矩形 | |
| B. | 有一组邻角是直角的四边形一定是矩形 | |
| C. | 对角线互相平分的四边形是矩形 | |
| D. | 对角互补的平行四边形是矩形 |
7.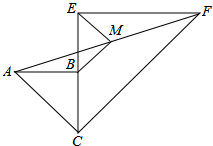 如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
(1)求证:MB∥CF;
(2)若CB=a,CE=2a,求BM,ME的长.
 如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
如图,两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)求证:MB∥CF;
(2)若CB=a,CE=2a,求BM,ME的长.
11.如果x=2是关于x的方程3-2x=x+a的解,那么a的值应是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为$\frac{2\sqrt{3}}{3}$.
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为$\frac{2\sqrt{3}}{3}$. 作图题(不写作法,保留作图痕迹).
作图题(不写作法,保留作图痕迹).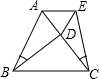 已知,如图△ABC为等边三角形,且∠ACE=∠ABD,CE=BD,试说明:
已知,如图△ABC为等边三角形,且∠ACE=∠ABD,CE=BD,试说明: