题目内容
3.小明在解决问题:已知a=$\frac{1}{2+\sqrt{3}}$,求2a2-8a+1的值他是这样分析与解的:∵a=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$,
∴a-2=-$\sqrt{3}$,∴(a-2)2=3,a2-4a+4=3
∴a2-4a=-1,2a2-8a+1=2(a2-4a)+1=2×(-1)+1=-1.
请你根据小明的分析过程,解决如下问题:
(1)化简$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{121}+\sqrt{119}}$
(2)若a=$\frac{1}{\sqrt{2}-1}$,求下面式的值①2a2-8a+1;②2a2-5a+$\frac{1}{a}$+2.
分析 (1)将原式分母有理化即可;
(2)将a分母有理化,化简为$\sqrt{2}$+1,代入①,②进行运算即可.
解答 解:(1)原式=$\frac{1}{2}$×($\sqrt{3}$+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+…+$\sqrt{121}$-$\sqrt{119}$)
=$\frac{1}{2}$×($\sqrt{121}$-1)
=$\frac{1}{2}$×10
=5;
(2)①∵a=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}+$1,
∴2a2-8a+1
=2×($\sqrt{2}+$1)2-8×($\sqrt{2}$+1)+1
=-6$\sqrt{2}$-1;
②2a2-5a+$\frac{1}{a}$+2
=2×($\sqrt{2}$+1)2-5($\sqrt{2}+$1)+2
=2.
点评 本题主要考查了分母有理化,利用分母有理化化简是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.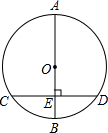 如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
 如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )| A. | 10cm | B. | 14cm | C. | 15cm | D. | 16cm |
11.一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
18.为了了解湖州市2017年中考数学学科各分数段成绩分布情况,从中抽取2000名考生的中考数学成绩进行统计分析,在这个问题中,样本是指( )
| A. | 2000 | |
| B. | 湖州市2017年中考数学成绩 | |
| C. | 被抽取的2000名考生 | |
| D. | 被抽取的2000名考生的中考数学成绩 |
8.已知10x=20,5x=8,则2x的值是( )
| A. | $\frac{2}{5}$ | B. | $\frac{5}{2}$ | C. | 12 | D. | 160 |
15.淮安市今年有43735名初三学生参加数学中考,从中抽取1000名考生的数学成绩进行分析,则在该调查中,样本指的是( )
| A. | 1000 | B. | 1000名 | ||
| C. | 43735名考生的数学成绩 | D. | 1000名考生的数学成绩 |
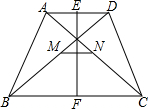 已知:如图,在四边形ABCD中,AD∥BC,AB=DC,E、F、M、N分别是AD、BC、BD、AC的中点,试说明:EF与MN互相垂直平分.
已知:如图,在四边形ABCD中,AD∥BC,AB=DC,E、F、M、N分别是AD、BC、BD、AC的中点,试说明:EF与MN互相垂直平分.