题目内容
19.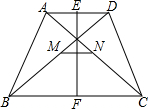 已知:如图,在四边形ABCD中,AD∥BC,AB=DC,E、F、M、N分别是AD、BC、BD、AC的中点,试说明:EF与MN互相垂直平分.
已知:如图,在四边形ABCD中,AD∥BC,AB=DC,E、F、M、N分别是AD、BC、BD、AC的中点,试说明:EF与MN互相垂直平分.
分析 连接ME、MF、NE、NF,证出ME是△ABD的中位线,由三角形中位线定理得出ME=$\frac{1}{2}$AB,同理:MF=$\frac{1}{2}$CD,EN=$\frac{1}{2}$CD,FN=$\frac{1}{2}$AB,证出ME=MF=EN=FN,得出四边形EMFN是菱形,由菱形的性质即可得出结论
解答  证明:连接ME、MF、NE、NF,如图所示:
证明:连接ME、MF、NE、NF,如图所示:
∵E,M分别是AD,BD的中点,
∴ME是△ABD的中位线,
∴ME=$\frac{1}{2}$AB,
同理:MF=$\frac{1}{2}$CD,EN=$\frac{1}{2}$CD,FN=$\frac{1}{2}$AB,
∵AB=DC,
∴ME=MF=EN=FN,
∴四边形EMFN是菱形,
∴EF与MN互相垂直且平分.
点评 本题考查了中点四边形,三角形中位线定理、菱形的判定与性质;熟练掌握三角形中位线定理,证明四边形EMFN是菱形是解决问题的关键

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
7.在?ABCD中,AB=3cm,BC=6cm,一组对边之间的距离为4cm,则另一组对边之间的距离为( )
| A. | 8cm | B. | 8cm或2cm | C. | 2cm | D. | 无法确定 |
14.要对大批量生产的商品进行检验,下列做法比较合适的是( )
| A. | 把所有商品逐渐进行检验 | |
| B. | 从中抽取1件进行检验 | |
| C. | 从中挑选几件进行检验 | |
| D. | 从中按抽样规则抽取一定数量的商品进行检验 |
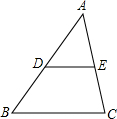 如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.
如图,若$\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}=\frac{3}{2}$,且△ABC的周长为36cm,则△ADE的周长为24cm.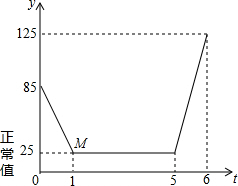 近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题:
近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题: 如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,若AO=8,BC=12,EO=$\sqrt{2}$BE,则线段OD=2$\sqrt{7}$,BE=4.
如图,D是⊙O弦BC的中点,A是弧BC上一点,OA与BC交于点E,若AO=8,BC=12,EO=$\sqrt{2}$BE,则线段OD=2$\sqrt{7}$,BE=4.