题目内容
7.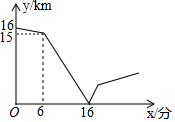 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.
分析 根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达A站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达B站需要的时间,再根据有理数的减法,可得答案.
解答 解:由纵坐标看出甲先行驶了1千米,由横坐标看出甲行驶1千米用了6分钟,
甲的速度是1÷6=$\frac{1}{6}$千米/分钟,
由纵坐标看出AB两地的距离是16千米,
设乙的速度是x千米/分钟,由题意,得
10x+16×$\frac{1}{6}$=16,
解得x=$\frac{4}{3}$千米/分钟,
相遇后乙到达A站还需(16×$\frac{1}{6}$)÷$\frac{4}{3}$=2分钟,
相遇后甲到达B站还需(10×$\frac{4}{3}$)÷$\frac{1}{6}$=80分钟,
当乙到达终点A时,甲还需80-2=78分钟到达终点B,
故答案为:78.
点评 本题考查了函数图象,利用同路程与时间的关系得出甲乙的速度是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.若一元二次方程2x2-6x+3=0的两根为x1,x2,则x1x2的值为( )
| A. | 3 | B. | 6 | C. | -6 | D. | $\frac{3}{2}$ |
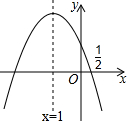 如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论:
如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点(0.5,0),有下列结论:
 如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.
如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.