题目内容
15.在平面直角坐标系xOy中,对于不在坐标轴上的任意一点P(x,y),我们把点P′($\frac{1}{x}$,$\frac{1}{y}$)称为点P的“倒影点”,直线y=-x+1上有两点A,B,它们的倒影点A′,B′均在反比例函数y=$\frac{k}{x}$的图象上.若AB=2$\sqrt{2}$,则k=-$\frac{4}{3}$.分析 设点A(a,-a+1),B(b,-b+1)(a<b),则A′($\frac{1}{a}$,$\frac{1}{1-a}$),B′($\frac{1}{b}$,$\frac{1}{1-b}$),由AB=2$\sqrt{2}$可得出b=a+2,再根据反比例函数图象上点的坐标特征即可得出关于k、a、b的方程组,解之即可得出k值.
解答 解:设点A(a,-a+1),B(b,-b+1)(a<b),则A′($\frac{1}{a}$,$\frac{1}{1-a}$),B′($\frac{1}{b}$,$\frac{1}{1-b}$),
∵AB=$\sqrt{(b-a)^{2}+[(-b+1)-(-a+1)]^{2}}$=$\sqrt{2(b-a)^{2}}$=$\sqrt{2}$(b-a)=2$\sqrt{2}$,
∴b-a=2,即b=a+2.
∵点A′,B′均在反比例函数y=$\frac{k}{x}$的图象上,
∴$\left\{\begin{array}{l}{b=a+2}\\{k=\frac{1}{a(1-a)}=\frac{1}{b(1-b)}}\end{array}\right.$,
解得:k=-$\frac{4}{3}$.
故答案为:-$\frac{4}{3}$.
点评 本题考查了反比例函数图象上点的坐标特征、一次函数图象上点的坐标特征以及两点间的距离公式,根据反比例函数图象上点的坐标特征列出关于k、a、b的方程组是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5.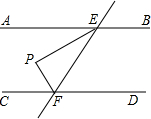 如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
 如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )
如图,AB∥CD,直线EF与AB、CD分别相交于E、F两点,EP平分∠AEF,过点F作FP⊥EP,若∠PEF=30°,则∠PFC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
6.估计-1+$\sqrt{23}$的值( )
| A. | 在4和5之间 | B. | 在3和4之间 | C. | 在2和3之间 | D. | 在1和2之间 |
3.某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:
下列说法正确的是( )
| 成绩/分 | 36 | 37 | 38 | 39 | 40 |
| 人数/人 | 1 | 2 | 1 | 4 | 2 |
| A. | 这10名同学体育成绩的中位数为38分 | |
| B. | 这10名同学体育成绩的平均数为38分 | |
| C. | 这10名同学体育成绩的众数为39分 | |
| D. | 这10名同学体育成绩的方差为2 |
20.据媒体报道,我国最新研制的“察打一体”无人机的速度极快,经测试最高速度可达204000米/分,这个数用科学记数法表示,正确的是( )
| A. | 204×103 | B. | 20.4×104 | C. | 2.04×105 | D. | 2.04×106 |
4.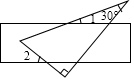 直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
 直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
16.计算$\sqrt{121×36}$等于( )
| A. | 45 | B. | 55 | C. | 66 | D. | 70 |
 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.
如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.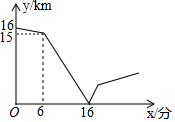 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.