题目内容
19. 如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.
如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.
分析 延长CD,交AE于点E,可得DE⊥AE,在直角三角形ABC中,由题意确定出AB的长,进而确定出EC的长,在直角三角形AED中,由题意求出ED的长,由EC-ED求出DC的长即可.
解答  解:延长CD,交AE于点E,可得DE⊥AE,
解:延长CD,交AE于点E,可得DE⊥AE,
在Rt△AED中,AE=BC=30m,∠EAD=30°,
∴ED=AEtan30°=10$\sqrt{3}$m,
在Rt△ABC中,∠BAC=30°,BC=30m,
∴AB=30$\sqrt{3}$m,
则CD=EC-ED=AB-ED=30$\sqrt{3}$-10$\sqrt{3}$=20$\sqrt{3}$m.
点评 此题考查了解直角三角形的应用-仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
14.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:
这15名员工每人所创年利润的众数、中位数分别是( )
| 部门 | 人数 | 每人所创年利润(单位:万元) |
| A | 1 | 10 |
| B | 3 | 8 |
| C | 7 | 5 |
| D | 4 | 3 |
| A. | 10,5 | B. | 7,8 | C. | 5,6.5 | D. | 5,5 |
4.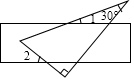 直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
 直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )
直角三角板和直尺如图放置,若∠1=20°,则∠2的度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |

 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.
如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是$\frac{\sqrt{3}}{18}$.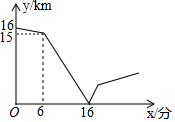 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.
甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需78分钟到达终点B.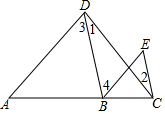 已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.
已知:如图,∠1=∠2,∠3=∠E.求证:AD∥BE.