题目内容
19.某商场销售的一款笔记本电脑按进价提高30%标价,在一次促销活动中,按标价的9折销售,同时顾客在该商场还可领取50元的购物券,这样每台电脑仍可盈利14.5%.(1)求这款电脑每台的进价.(利润率=$\frac{利润}{进价}$=$\frac{售价-进价}{进价}$)
(2)在这次促销活动中,商场销售了这款电脑80台,问:赢利多少元?
分析 (1)设一台电脑的进价为x元,根据利润率=$\frac{售价-进价}{进价}$列方程求解即可;
(2)先求得一台的利润,然后根据总利润=每台的利润×台数求解即可.
解答 解:(1)设一台电脑的进价为x元.
根据题意得:$\frac{90%×(1+30%)-50-x}{x}$=14.5%.
解得:x=2000元.
答:这款电脑每台的进价为2000元.
(2)2000×14.5%×80=23200元.
答:共盈利23200元.
点评 本题主要考查的是分式方程的应用,根据利润率=$\frac{售价-进价}{进价}$列出关于x的方程是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.下列函数的图象中与一次函数y=-2x+2的图象相交于点(1,0)的是( )
| A. | y=x+1 | B. | y=x-1 | C. | y=-4x+1 | D. | y=4x+1 |
14.用配方法解一元二次方程:-$\sqrt{2}$x2-2x+$\sqrt{6}$=0,可将方程化为( )
| A. | x2+$\sqrt{2}$x=-$\sqrt{3}$ | B. | x2-$\sqrt{2}$x=$\sqrt{3}$ | C. | x2+$\sqrt{2}$x=$\sqrt{3}$ | D. | x2-$\sqrt{2}$x=-$\sqrt{3}$ |
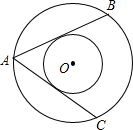 如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB为小圆的切线,则AC与小圆相切吗?请说明理由.
如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB为小圆的切线,则AC与小圆相切吗?请说明理由. 如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长.
如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长.