题目内容
7.已知,在△ABC中,∠ABC=90°,AD⊥BC于D,BD=6,CD=2,求tanC和sinB的值.分析 根据余角的性质得到∠C=∠BAD,推出△ACD∽△ABD,根据相似三角形的性质得到$\frac{AD}{CD}=\frac{BD}{AD}$,∠B=∠CAD,于是得到AD=$\sqrt{CD•BD}$=2$\sqrt{3}$,AC=4,根据锐角三角函数的定义即可得到结论.
解答  解:如图,∵∠ABC=90°,AD⊥BC于D,
解:如图,∵∠ABC=90°,AD⊥BC于D,
∴∠C+∠CAD=∠CAD+∠BAD=90°,
∴∠C=∠BAD,
∴△ACD∽△ABD,
∴$\frac{AD}{CD}=\frac{BD}{AD}$,∠B=∠CAD,
∴AD=$\sqrt{CD•BD}$=2$\sqrt{3}$,
∴AC2=CD•BC=16,
∴AC=4,
∴tanC=$\frac{AD}{CD}$=$\sqrt{3}$,
sinB=$\frac{AC}{AB}$=$\frac{1}{2}$.
点评 本题考查了解直角三角形,锐角三角函数的定义,相似三角形的判定和性质,弄清楚直角三角形中的边角关系是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.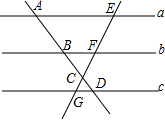 如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )
如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )
 如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )
如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )| A. | EC:CG=5:1 | B. | EF:FC=1:1 | C. | EF:FC=3:2 | D. | EF:EC=3:5 |
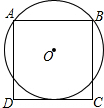 如图,⊙O过正方形ABCD的顶点A、B,且与CD相切.若正方形ABCD的边长为2,则⊙O的半径为$\frac{5}{4}$.
如图,⊙O过正方形ABCD的顶点A、B,且与CD相切.若正方形ABCD的边长为2,则⊙O的半径为$\frac{5}{4}$.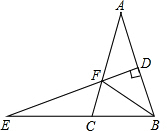 如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.
如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.