题目内容
设点A是抛物线y=x2-3x上位于x轴下方,且在对称轴左侧的一个动点,过点A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.
(1)当DC=1时,求矩形ABCD的周长;
(2)试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时点A的坐标;如果不存在,请说明理由.
(1)当DC=1时,求矩形ABCD的周长;
(2)试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时点A的坐标;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)先根据抛物线的解析式求出抛物线与x轴另一交点E的坐标,根据抛物线和矩形的对称性可知:OB的长,就是OE与BC的差的一半,由此可求出OB的长,即B点的坐标,然后代入抛物线的解析式中即可求出B点纵坐标,也就得出了矩形AB边的长.进而可求出矩形的周长;
(2)思路同(1)可设出A点坐标(设横坐标,根据抛物线的解析式表示纵坐标),也就能表示出B点的坐标,即可得出OB的长,同(1)可得出BC的长,而AB的长就是A点纵坐标的绝对值,由此可得出一个关于矩形周长和A点纵坐标的函数关系式,根据函数的性质可得出矩形周长的最大值及对应的A的坐标.
(2)思路同(1)可设出A点坐标(设横坐标,根据抛物线的解析式表示纵坐标),也就能表示出B点的坐标,即可得出OB的长,同(1)可得出BC的长,而AB的长就是A点纵坐标的绝对值,由此可得出一个关于矩形周长和A点纵坐标的函数关系式,根据函数的性质可得出矩形周长的最大值及对应的A的坐标.
解答:解:(1)由y=x2-3x,
令y=0,得x2-3x=0,
解得x1=0,x2=3
∴抛物线与x轴的另一个交点为(3,0)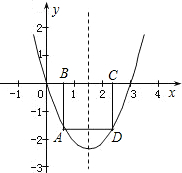
∴它的顶点为(
,
),对称轴为直线x=
,其大致位置如图所示,
∵BC=1,易知OB=
×(3-1)=1.
∴B(1,0)
∴点A的横坐标x=1,又点A在抛物线y=x2-3x上,
∴点A的纵坐标y=12-3×1=-2.
∴AB=|y|=|-2|=2.
∴矩形ABCD的周长为:2(AB+BC)=2×(2+1)=6.
(2)∵点A在抛物线y=x2-3x上,故可设A点的坐标为(x,x2-3x),
∴B点的坐标为(x,0).(0<x<
)
∴BC=3-2x,A在x轴下方,
∴x2-3x<0,
∴AB=|x2-3x|=3x-x2
∴矩形ABCD的周长,
C=2[(3x-x2)+(3-2x)]=-2(x-
)2+
,
∵a=-2<0,抛物线开口向下,二次函数有最大值,
∴当x=
时,矩形ABCD的周长C最大值为
.
此时点A的坐标为A(
,-
).
令y=0,得x2-3x=0,
解得x1=0,x2=3
∴抛物线与x轴的另一个交点为(3,0)

∴它的顶点为(
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
∵BC=1,易知OB=
| 1 |
| 2 |
∴B(1,0)
∴点A的横坐标x=1,又点A在抛物线y=x2-3x上,
∴点A的纵坐标y=12-3×1=-2.
∴AB=|y|=|-2|=2.
∴矩形ABCD的周长为:2(AB+BC)=2×(2+1)=6.
(2)∵点A在抛物线y=x2-3x上,故可设A点的坐标为(x,x2-3x),
∴B点的坐标为(x,0).(0<x<
| 3 |
| 2 |
∴BC=3-2x,A在x轴下方,
∴x2-3x<0,
∴AB=|x2-3x|=3x-x2
∴矩形ABCD的周长,
C=2[(3x-x2)+(3-2x)]=-2(x-
| 1 |
| 2 |
| 13 |
| 2 |
∵a=-2<0,抛物线开口向下,二次函数有最大值,
∴当x=
| 1 |
| 2 |
| 13 |
| 2 |
此时点A的坐标为A(
| 1 |
| 2 |
| 5 |
| 4 |
点评:本题主要考查二次函数的综合知识,重点考查二次函数解析式的确定以及二次函数的应用,难度适中,是一道好题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=55°,则∠AEF为多少度?
如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=55°,则∠AEF为多少度? 在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F.
在△ABC中,P是BC边上的一个动点,以AP为直径的⊙O分别交AB、AC于点E和点F. 如图所示,已知AB=CD,BC=DA,求证:AB∥CD,BC∥DA.
如图所示,已知AB=CD,BC=DA,求证:AB∥CD,BC∥DA. 如图,∠AOC=∠BOD=90°,且∠AOB=162°,则∠COD=
如图,∠AOC=∠BOD=90°,且∠AOB=162°,则∠COD= 如图,已知二次函数y=-
如图,已知二次函数y=-