题目内容
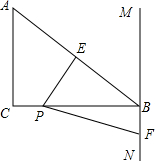 在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作直线MN∥AC,点P在直线AC上,∠EPF=∠CAB,且两边分别交直线AB于E,交直线MN于F,如图,探究PE与PF之间的数量关系.
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作直线MN∥AC,点P在直线AC上,∠EPF=∠CAB,且两边分别交直线AB于E,交直线MN于F,如图,探究PE与PF之间的数量关系.考点:相似三角形的判定与性质
专题:常规题型
分析:作PK⊥AB,垂足为K,可证△PKE∽△PBF,可证△ACB∽△PKB即可解题.
解答:解:作PK⊥AB,垂足为K,

∵∠C=90°,∠AKP=90°
∴∠A+∠CPK=180°
∵∠CPK+∠KPB=180°,
∴∠A=∠KPB,
∵∠A=∠EPF,
∴∠KPE=∠FPB,
∵∠PKE=∠PBF=90°
∴△PKE∽△PBF
∴PE:PF=PK:PB
∴△ACB∽△PKB,
∴PK:AC=PB:AB
∴PK:PB=AC:AB=3:5,
∴PE:PF=3:5.

∵∠C=90°,∠AKP=90°
∴∠A+∠CPK=180°
∵∠CPK+∠KPB=180°,
∴∠A=∠KPB,
∵∠A=∠EPF,
∴∠KPE=∠FPB,
∵∠PKE=∠PBF=90°
∴△PKE∽△PBF
∴PE:PF=PK:PB
∴△ACB∽△PKB,
∴PK:AC=PB:AB
∴PK:PB=AC:AB=3:5,
∴PE:PF=3:5.
点评:本题考查了相似三角形的判定,考查了相似三角形的对应边比值相等的性质.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
在下面各数中无理数的个数有( )
|-
|,-3.14,
,0.1010010001…,+1.99,-
.
|-
| 3 |
| 4 |
| 22 |
| 7 |
| π |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
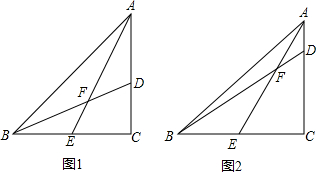 在△ABC中,AC=BC,∠ACB=90°,E是线段BC的中点,D在边AC上,线段BD和AE交于点F.
在△ABC中,AC=BC,∠ACB=90°,E是线段BC的中点,D在边AC上,线段BD和AE交于点F.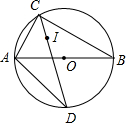 如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD.
如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD.