题目内容
18.如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中相邻两个正方形的间距都是1,则点A2017的坐标为( )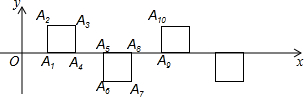
| A. | (1008,1) | B. | (1009,0) | C. | (1010,0) | D. | (1009,1) |
分析 根据横坐标,纵坐标的变化规律,每8个点看作一次循环,再根据点A2017在第253个循环中的第一个点的位置,即可得出点A2017的坐标.
解答 解:由图可得,第一个正方形中,A1(1,0),A2(1,1),A3(2,1),A4(2,0),各点的横坐标依次为1,1,2,2,纵坐标依次为0,1,1,0;
第二个正方形中,A5(3,0),A6(3,-1),A7(4,-1),A8(4,0),各点的横坐标依次为3,3,4,4,纵坐标依次为0,-1,-1,0;
根据纵坐标的变化规律可知,每8个点一次循环,
∵2016÷8=252,
∴点A2017在第253个循环中的第一个点的位置,故其纵坐标为0,
又∵A1的横坐标为1,A9的横坐标为5=1+4×1,A17的横坐标为9=1+4×2,…
∴A2017的横坐标为1+4×(253-1)=1009,
∴点A2017的坐标为(1009,0),
故选:B.
点评 本题主要考查了点的坐标变化规律问题以及正方形的性质的运用,解决问题的关键是判断点A2017在第253个循环中的第一个点的位置.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
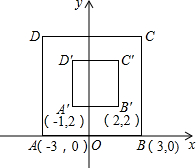 如图,在平面直角坐标xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每一个点的横,纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A、B的对应点分别为A′、B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,则点F的坐标为(1,4).
如图,在平面直角坐标xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每一个点的横,纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A、B的对应点分别为A′、B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,则点F的坐标为(1,4). 如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.
如图,CE是△ABC的外角∠ACD的平分线,交BA的延长线于点E,若∠E=20°,∠B=30°,则∠BAC=70°.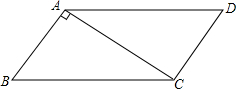 如图:在?ABCD中,CA⊥BA,AB=3,AC=4,求?ABCD的周长及面积.
如图:在?ABCD中,CA⊥BA,AB=3,AC=4,求?ABCD的周长及面积.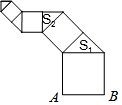 按如图所示的方式作正方形和等腰直角三角形,若第一个正方形的边AB=1,第1个等腰直角三角形面积为S1,第2个等腰直角三角形的面积为S2,…,第n个等腰直角三角形的面积为Sn(其中n为正整数),则Sn=$\frac{1}{{2}^{n+1}}$.
按如图所示的方式作正方形和等腰直角三角形,若第一个正方形的边AB=1,第1个等腰直角三角形面积为S1,第2个等腰直角三角形的面积为S2,…,第n个等腰直角三角形的面积为Sn(其中n为正整数),则Sn=$\frac{1}{{2}^{n+1}}$.