题目内容
6.观察下列各式:1×3-22=-1
2×4-32=-1
3×5-42=-1
…
(1)分别计算出上述三个式子的结果,并填写在横线处.
(2)请试着写出满足这种关系的第四个式子:4×6-52=-1
(3)通过观察和计算,请把这个规律用含字母n(n为正整数)的式子表示出来n×(n+2)-(n+1)2=-1.
分析 (1)分别计算出三个式子,即可得出结论;
(2)观察前三个等式,根据数的变化找出第四个式子;
(3)根据等式中数的变化,找出第n个等式为n×(n+2)-(n+1)2=-1,此题得解.
解答 解:(1)1×3-22=3-4=-1;2×4-32=8-9=-1;3×5-42=15-16=-1.
故答案为:-1;-1;-1.
(2)观察等式左边:1、3、2,2、4、3,3、5、4;
等式右边:-1,-1,-1.
∴第四个式子左边:4、6、5,右边:-1.
即4×6-52=-1.
故答案为:4×6-52=-1.
(3)∵1×3-22=-1;2×4-32=-1;3×5-42=-1,4×6-52=-1,…,
∴第n个式子为:n×(n+2)-(n+1)2=-1.
故答案为:n×(n+2)-(n+1)2=-1.
点评 本题考查了规律型中数的变化类,根据等式中数的变化找出变化规律“n×(n+2)-(n+1)2=-1”是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
16.下列关系式中,不含有x=-1这个解的是( )
| A. | 2x+1=-1 | B. | 2x+1>-1 | C. | -2x+1≥3 | D. | -2x-1≤3 |
18.如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中相邻两个正方形的间距都是1,则点A2017的坐标为( )
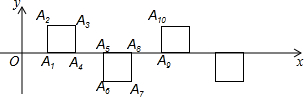

| A. | (1008,1) | B. | (1009,0) | C. | (1010,0) | D. | (1009,1) |
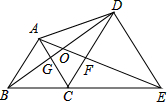 如图所示,点B、C、E在同一直线上,△ABC与△CDE都是等边三角形,则下列所有正确的结论序号为①②③⑥
如图所示,点B、C、E在同一直线上,△ABC与△CDE都是等边三角形,则下列所有正确的结论序号为①②③⑥