题目内容
已知：如图，在△DBC中，BC=DC，过点C作CE⊥DC交DB的延长线于点E，过点C作AC⊥BC且AC=EC，连结AB．求证：AB=ED．
考点：全等三角形的判定与性质
专题：证明题
分析：根据垂直的定义可得∠DCE=∠BAC=90°，然后利用“边角边”证明△ABC和△EDC全等，再根据全等三角形对应边相等证明即可．
解答：证明：∵CE⊥DC，AC⊥BC，
∴∠DCE=∠BAC=90°，
在△ABC和△EDC中，
，
∴△ABC≌△EDC（SAS），
∴AB=ED．
∴∠DCE=∠BAC=90°，
在△ABC和△EDC中，
|
∴△ABC≌△EDC（SAS），
∴AB=ED．
点评：本题考查了全等三角形的判定与性质，是基础题，熟练掌握全等三角形的判定方法是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
点M（-2，1）关于x轴对称的点的坐标是（ ）
| A、（-2，-1） |
| B、（2.1） |
| C、（2，-1） |
| D、（1．-2） |
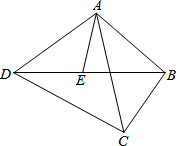已知：如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE．
如图，已知在△ABC中，AB=AC，BC=8，tan∠ABC=3，AD⊥BC于D，O是AD上一点，OD=3，以OB为半径的⊙O分别交AB、AC于E、F．求：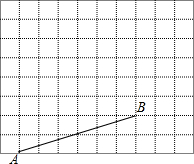
如图所示是10×8的网格，网格中每个小正方形的边长均为1，A、B两点在小正方形的顶点上，使以A、B、C为顶点的三角形分别满足以下要求：