题目内容
6. 如图,正方形ABCD与正△AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是15°或165°.
如图,正方形ABCD与正△AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是15°或165°.
分析 先根据BE=DF,AE=AF,AB=AD判定△ABE≌△ADF,再根据∠BAE的位置求得其度数.
解答 解:①如图,当正△AEF在正方形ABCD内部时,
由BE=DF,AE=AF,AB=AD可得△ABE≌△ADF
∴∠BAE=∠DAF=$\frac{1}{2}$(90°-60°)=15°
②如图,当正△AEF在正方形ABCD外部时,
由BE=DF,AE=AF,AB=AD可得△ABE≌△ADF
∴∠BAE=∠DAF=$\frac{1}{2}$(360°-90°+60°)=165°
故答案为:15°或165°
点评 本题主要考查了正方形和等边三角形的性质,解决问题的关键是掌握全等三角形的判定方法.在求∠BAE的度数时,需要分两种情况进行讨论.

练习册系列答案
相关题目
14.若A(3,y1),B(5,y2),C(-2,y3)是抛物线y=-x2+4x+k上的三点,则y1、y2、y3的大小关系为( )
| A. | y2>y1>y3 | B. | y3>y2>y1 | C. | y1>y2>y3 | D. | y3>y1>y2 |
18.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 锐角三角形或钝角三角形 |
15.下列说法中正确的是( )
| A. | “作线段CD=AB”是一个命题 | |
| B. | 三角形的三条内角平分线交于一点 | |
| C. | 命题“若x=1,则x2=1”的逆命题是真命题 | |
| D. | 命题“两直线平行,内错角相等”的逆命题是假命题 |
16.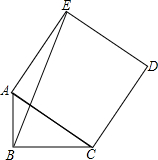 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )
 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,以斜边AC为边作正方形ACDE,连接BE,则BE的长是( )| A. | $2\sqrt{58}$ | B. | 14 | C. | $2\sqrt{65}$ | D. | $4\sqrt{13}$ |
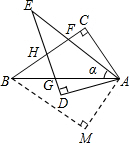 如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.
如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H. 在平面直角坐标系xOy中,已知抛物线y=a(x+1)2+c(a>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其顶点为M,若直线MC的函数表达式为y=kx-3,与x轴的交点为N,且cos∠BCO=$\frac{3\sqrt{10}}{10}$.
在平面直角坐标系xOy中,已知抛物线y=a(x+1)2+c(a>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其顶点为M,若直线MC的函数表达式为y=kx-3,与x轴的交点为N,且cos∠BCO=$\frac{3\sqrt{10}}{10}$.