题目内容
17.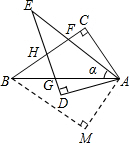 如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.
如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.(1)求证:△ACB≌△AMB;
(2)若α=30°,求证:四边形ADHC是正方形;
(3)若∠AFG=70°,求α的值.
分析 (1)根据已知利用全等三角形的判定定理AAS定理可得结论;
(2)由旋转可知∠MAD=30°,利用角的加减可得∠GADD=30°,易得∠CAD=90°,又因为∠CCC=∠DD=90°,由矩形的判定定理可知四边形ADADHC是矩形,由全等三角形的性质和旋转的性质可得AC=AD,利用正方形的判定定理可得结论;
(3)连接FFG,利用全等三角形的性质和旋转的性质可得∠CAB=∠DAE,易得∠CCAF=∠GADG,易得△ACFACF≌△ADGAAD,由全等三角形的性质定理可得AAF=AAG,利用三角形的内角和定理可得结果.
解答 (1)证明:△ACB与△AMB中,
$\left\{\begin{array}{l}{∠C=∠M=90°}\\{∠CAB=∠MAB=60°}\\{BA=BA}\end{array}\right.$,
∴△ACB≌△AMB(AAS);
(2)证明:当α=30°时,∠MADMAD=30°,
∵∠CABCAB=∠MMAB=60°,
∴∠GADD=30°,
∴∠CADCA=90°.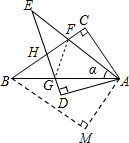
∴四边形ADADHC是矩形.
∵△AACB≌△AMBA,
∴AAC=AM=ADA,
∴四边形AADHC是正方形;
(3)解:如右图,连接FFG,
∵∠CAF+∠FABF=∠GADG+∠FABF,
∴∠CCAF=∠GADG,
在△ACFACF和△ADG中AAD,
$\left\{\begin{array}{l}{∠CAF=∠GAD}\\{AC=AD}\\{∠C=∠D}\end{array}\right.$,
∴△ACFACF≌△ADGAAD(ASA),
∴AAF=AAG,
∴∠AGFA=∠AAFG=70°,
∴α=40°.
点评 本题主要考查了全等三角形的判定及性质定理,利用旋转的性质得到全等的条件是解答此题的关键.

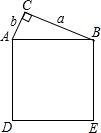 已知:如图,△ACB的面积为30,∠C=90°,BC=a,AC=b,正方形ADEB的面积为169,则(a-b)2的值为( )
已知:如图,△ACB的面积为30,∠C=90°,BC=a,AC=b,正方形ADEB的面积为169,则(a-b)2的值为( )| A. | 25 | B. | 49 | C. | 81 | D. | 100 |
 如图,△ABC中,AB=AC,ED是腰AB的垂直平分线,∠DBC=30°,求∠A的度数.
如图,△ABC中,AB=AC,ED是腰AB的垂直平分线,∠DBC=30°,求∠A的度数. 如图,在△ABC中,∠B=30°,BC的垂直平分线交边AB于E,垂足为D,连接CE,若ED=3,则CE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交边AB于E,垂足为D,连接CE,若ED=3,则CE的长为( ) 如图,在平面直角坐标系中,点A在坐标原点,∠CAB=45°,AC=2$\sqrt{2}$,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.
如图,在平面直角坐标系中,点A在坐标原点,∠CAB=45°,AC=2$\sqrt{2}$,∠ACB=60°,点B在x轴正半轴,点C在第一象限,动点D在边AB上运动,以CD为直径作⊙O与AC,AB分别交于E,F,连接EF.



 如图,正方形ABCD与正△AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是15°或165°.
如图,正方形ABCD与正△AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是15°或165°.