Question

10．如图，已知二次函数y=-$\frac{1}{2}$x²+bx+c的图象经过A（6，0），B（0，-6）两点．
（1）求这个二次函数的解析式；
（2）设抛物线的顶点为M，求△MAB的面积；
（3）设抛物线与x轴的另一交点为C，求证：MC∥AB．

Answer 1

分析 （1）直接利用待定系数法求出b，c的值进而得出答案；
（2）直接利用配方法求出M点坐标，再求出直线AB的解析式，得出N点坐标，进而得出MN的长，即可得出△MAB的面积；
（3）首先求出直线CM的解析式，进而利用斜率关系得出直线位置关系．

解答 （1）解：将A（6，0），B（0，-6）两点代入二次函数y=-$\frac{1}{2}$x²+bx+c得：
$\left\{\begin{array}{l}{-\frac{1}{2}×{6}^{2}+6b+c=0}\\{c=-6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=4}\\{c=-6}\end{array}\right.$，
故这个二次函数的解析式为：y=-$\frac{1}{2}$x²+4x-6；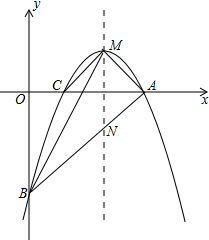

（2）解：y=-$\frac{1}{2}$x²+4x-6
=-$\frac{1}{2}$（x²-8x）-6
=-$\frac{1}{2}$（x-4）²+2，
故M点的坐标为：（4，2），
设直线AB的解析式为：y=kx+d，
则$\left\{\begin{array}{l}{6k+d=0}\\{d=-6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=1}\\{d=-6}\end{array}\right.$，
故直线AB的解析式为：y=x-6，
故x=4时，y=-2，
则N点纵坐标为：-2，即MN=2-（-2）=4，
故△MAB的面积为：$\frac{1}{2}$×4×AO=12；

（3）证明：∵M（4，2），A（6，0），
∴C（2，0），
设直线CM的解析式为：y=ex+f，
则$\left\{\begin{array}{l}{2e+f=0}\\{4e+f=2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{e=1}\\{f=-2}\end{array}\right.$，
故直线CM的解析式为：y=x-2，
可得直线AB与直线CM平行，即MC∥AB．

点评 此题主要考查了抛物线与x轴交点以及待定系数法求一次函数和二次函数解析式，正确求出函数解析式是解题关键．