题目内容
2.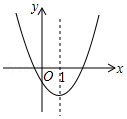 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.①b2>4ac;
②4a+2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 ①根据抛物线与x轴有交点,即可判定正确.
②由图象可知,x=2时,y<0,即可判定正确.
③错误,不等式ax2+bx+c>0的解集是x<x1或x>x2(x1,x2分别抛物线与x轴解得的横坐标,x1是左交点横坐标).
④根据点(5,y2)分、到对称轴的距离比点(-2,y1)到对称轴的距离大,即可判定正确.
解答 解:∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴b2>4ac,故①正确,
由图象可知,x=2时,y<0,
∴4a=2b+c<0,故②正确,
由图象可知,不等式ax2+bx+c>0的解集是x<x1或x>x2(x1,x2分别抛物线与x轴解得的横坐标,x1是左交点横坐标),故③错误,
由图象可知,点(5,y2)分、到对称轴的距离比点(-2,y1)到对称轴的距离大,
∴y2>y1,故④正确.
故选B.
点评 本题考查二次函数的应用,解题的关键是熟练掌握二次函数的有关性质,属于中考常考题型.

练习册系列答案
相关题目
10.成年人一年心跳的正常次数约为36792000次,用科学记数法表示为( )
| A. | 3.6792×108 | B. | 3679.2×104 | C. | 3.6792×107 | D. | 0.36792×108 |
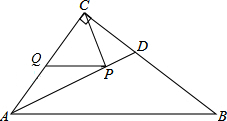 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4.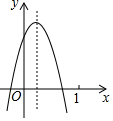 二次函数y=ax2+bx+c(a≠0)的图象如图,结论:①ac<0;②a-b+c<0;③b2-4ac≥0;④y随x的增大而增大,其中正确的个数( )
二次函数y=ax2+bx+c(a≠0)的图象如图,结论:①ac<0;②a-b+c<0;③b2-4ac≥0;④y随x的增大而增大,其中正确的个数( )