若关于x的分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=$\frac{3}{x+2}$有增根.则m的值是( )A．1B．-4或6C．6或1D．1或-4或6 题目和参考答案——青夏教育精英家教网—

题目内容

20．若关于x的分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=$\frac{3}{x+2}$有增根，则m的值是（　　）

A．

B．

-4或6

C．

6或1

D．

1或-4或6

分析增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．把增根代入化为整式方程的方程即可求出m的值．

解答解：方程两边都乘（x+2）（x-2），得
2（x+2）+mx=3（x-2），
∵原方程有增根，
∴最简公分母（x+2）（x-2）=0，
解得x=-2或2．
把x=-2代入整式方程，得-2m=-12，解得m=6；
把x=2代入整式方程，得8+2m=0，解得m=-4．
故选B．

点评本题考查了分式方程的增根，增根确定后可按如下步骤进行：
①化分式方程为整式方程；
②把增根代入整式方程即可求得相关字母的值．

练习册系列答案

11．已知抛物线y=x²+bx+c经过点B，与y轴交于点A，顶点P在直线OB上．

（1）如图1，若点B的坐标为（3，6），点P的横坐标为1，试确定抛物线的函数表达式；
（2）在（1）的条件下，若点M是直线AB下方抛物线上的一点，且S_△ABM=3，求点M的坐标；
（3）如图2，若点P在第一象限，且PA=PO，过点P作PD⊥x轴于点D．将抛物线y=x²+bx+c平移，平移后的抛物线经过A，D两点，与x轴的另一个交点为C．问：如何平移抛物线y=x²+bx+c，使四边形OABC为正方形？

8．在直角坐标系中A（-1，0），B（3，0），C（1，3），以A、B、C、D为顶点的四边形是平行四边形，则点D的坐标为此题答案不唯一，如（-3，3）．（写出一个）

$\frac{2x}{{x}^{2}+1}$

C．

$\frac{x-1}{{x}^{2}-1}$

D．

$\frac{1-x}{x-1}$

5．若x²+6x+□是一个完全平方式，那么□上应该填入的数字为9．

12．计算：16×2^-4=1．

9．

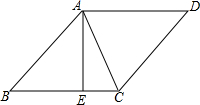如图，在菱形ABCD中，AB=5，对角线AC=6，过A作AE⊥BC，垂足为E，则AE的长是（　　）

10．

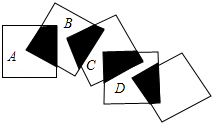将五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和是（　　）cm²．

试题分类