题目内容
12.已知一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象的一个交点为P(a,b),且P到原点的距离为$\sqrt{10}$,求反比例函数的解析式及a,b的值.分析 根据题意和交点坐标的意义可知,b=a+2,a2+b2=10,联立程组求解即可得到a,b的值,进而根据k=ab,得出k的值.
解答 解:由题意得
$\left\{\begin{array}{l}{b=a+2}\\{{a}^{2}+{b}^{2}=10}\end{array}\right.$
解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{{b}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{a}_{2}=-3}\\{{b}_{2}=-1}\end{array}\right.$,
∴k=ab=3.
故a=1,b=3或a=-3,b=-1,反比例函数的解析式为y=$\frac{3}{x}$.
点评 本题综合考查了两点间的距离公式以及解一元二次方程的综合应用.根据解析式组成的方程组求出交点的坐标是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列运算正确的是( )
| A. | 2÷$\sqrt{2}$=$\frac{1}{2}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | (-$\sqrt{2}$)2=-2 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
3.下列说法中正确的是( )
| A. | 正整数与正分数统称为正有理数 | B. | 正整数与负整数统称为整数 | ||
| C. | 正分数、0、负分数统称为分数 | D. | 一个有理数不是正数就是负数 |
17.若直角三角形两边长分别是6,8,则它的斜边为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 以上都不正确 |
 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π)
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$(结果保留π) 如图,一张长方形纸片ABCD沿EF折叠,若∠DEF=110°,∠DEA=40度.
如图,一张长方形纸片ABCD沿EF折叠,若∠DEF=110°,∠DEA=40度.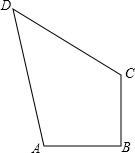 如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )
如图,在四边形ABCD中,AB=BC=2,DC=$3\sqrt{2}$,AD=$\sqrt{26}$,∠ABC=90°,则四边形ABCD的面积是( )