题目内容
13. 如图,在△ABC中,AD平分∠BAC,CE⊥AD于点O,交AB于点E,试说明DE与DC的关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,CE⊥AD于点O,交AB于点E,试说明DE与DC的关系,并说明理由.
分析 由角平分线的定义得到∠EAO=∠CAO,由于CE⊥AD于点O,求得∠AOE=∠AOC=90°,推出△AOE≌△AOC,得到OE=OC,证得AD垂直平分CE,根据线段垂直平分线的性质即可得到结论.
解答 解:∵AD平分∠BAC,
∴∠EAO=∠CAO,
∵CE⊥AD于点O,
∴∠AOE=∠AOC=90°,
在△AOE与△AOC中,
$\left\{\begin{array}{l}{∠EAO=∠CAO}\\{AO=AO}\\{∠AOE=∠AOC}\end{array}\right.$,
∴△AOE≌△AOC,
∴OE=OC,
∴AD垂直平分CE,
∴CD=ED.
点评 本题考查了等腰三角形的判定和性质,线段垂直平分线的性质,全等三角形的判定和性质,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.若字母a表示任意一个数,则-a表示的数是( )
| A. | 正数 | B. | 负数 | ||
| C. | 0 | D. | 以上情况都有可能 |
 如图,在△ABC中,AB=8,BC=10,∠BAC、∠BCA的平分线相交于点O,过点O的直线DE∥AC,分别交AB、BC于点D,求△BDE的周长.
如图,在△ABC中,AB=8,BC=10,∠BAC、∠BCA的平分线相交于点O,过点O的直线DE∥AC,分别交AB、BC于点D,求△BDE的周长. 如图所示,在平面直角坐标系中,点P(1,0)作如下实验:先向上平移(后一次平移比上一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位得到点P1,作点P1关于原点的对称点P2,再向上平移2个单位得到P3,作P3关于原点的对称点P4…,那么点P2015的坐标是(-1,504).
如图所示,在平面直角坐标系中,点P(1,0)作如下实验:先向上平移(后一次平移比上一次多1个单位长度),再作关于原点的对称点,即向上平移1个单位得到点P1,作点P1关于原点的对称点P2,再向上平移2个单位得到P3,作P3关于原点的对称点P4…,那么点P2015的坐标是(-1,504).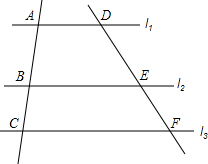 如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,DE=4,EF=2,则:
如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,DE=4,EF=2,则: 一块矩形耕地大小尺寸如图所示,要在这块地上沿东西南北方向分别挖4条和3条水渠,如果水渠的宽相等,而且要保证余下的可耕地而积为8700m2,那么水渠要挖多宽?
一块矩形耕地大小尺寸如图所示,要在这块地上沿东西南北方向分别挖4条和3条水渠,如果水渠的宽相等,而且要保证余下的可耕地而积为8700m2,那么水渠要挖多宽?