题目内容
5.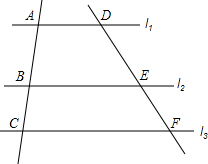 如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,DE=4,EF=2,则:
如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,DE=4,EF=2,则:①BC:AB=$\frac{1}{2}$;
②AB:AC=$\frac{2}{3}$;
③BC•DE=6;
④BC•EF=12.
分析 根据平行线分线段成比例定理得出 ①$\frac{BC}{AB}=\frac{EF}{DE}$,②$\frac{AB}{AC}=\frac{DE}{DF}$,③BC•DE=AB•EF,代入数据即可得到结论,④把BC、EF的值代入BC•EF求出即可.
解答 解:∵l1∥l2∥l3,
∴①$\frac{BC}{AB}=\frac{EF}{DE}$=$\frac{2}{4}$=$\frac{1}{2}$;
②$\frac{AB}{AC}=\frac{DE}{DF}$=$\frac{4}{6}$=$\frac{2}{3}$;
③$\frac{BC}{AB}=\frac{EF}{DE}$,
∴BC•DE=AB•EF=3×2=6;
④BC•EF═6×2=12.
故答案为:$\frac{1}{2}$,$\frac{2}{3}$,6,12.
点评 本题考查了平行线分线段成比例定理,找准对应线段是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若3a=2b=4c,且abc≠0,则$\frac{a+b}{c-2a}$的值是( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
 如图,在△ABC中,AD平分∠BAC,CE⊥AD于点O,交AB于点E,试说明DE与DC的关系,并说明理由.
如图,在△ABC中,AD平分∠BAC,CE⊥AD于点O,交AB于点E,试说明DE与DC的关系,并说明理由.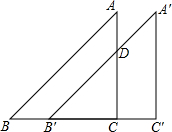 等腰直角三角形ABC中,AC=BC=10厘米,将三角形沿BC方向平移4厘米,得到等腰三角形A′B′C′,那么四边形ABB′D的面积=32平方厘米.
等腰直角三角形ABC中,AC=BC=10厘米,将三角形沿BC方向平移4厘米,得到等腰三角形A′B′C′,那么四边形ABB′D的面积=32平方厘米.