题目内容
1．求当x-9不小于-x+7时，x的取值范围．分析 利用x-9不小于-x+7得不等式x-9≥-x+7，然后解一元一次不等式即可．
解答 解：根据题意得x-9≥-x+7，
移项得x+x≥9+7，
合并得2x≥16，
系数化为1得x≥8，
即x的取值范围为x≥8．
点评 本题考查了解一元一次不等式：根据不等式的性质解一元一次不等式，基本操作方法与解一元一次方程基本相同，都有如下步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
11．比-6.1大，而比1小的整数的个数是（ ）
| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
12．小芳妈妈要给一幅长为60cm，宽为40cm的矩形十字绣的四周装裱一条宽度相同的金色边框制成一幅矩形挂图，使整幅挂图面积是3400cm2．设金色边框的宽度为x cm，则x满足的方程是（ ）
| A． | x2+50x-1400=0 | B． | x2-65x-250=0 | C． | x2-30x-1400=0 | D． | x2+50x-250=0 |
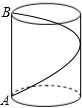如图，有一圆柱油罐，已知油罐的底面圆的周长是12米，高是5米，要从点A起环绕油罐建梯子，梯子的顶端正好到达点A的正上方点B，则梯子最短需多长？
如图所示，已知：DE∥BC，∠DEB=∠GFC．求证：BE∥FG．
如图，在△ABC中，AD平分∠BAC，CE⊥AD于点O，交AB于点E，试说明DE与DC的关系，并说明理由．
10．若3a=2b=4c，且abc≠0，则$\frac{a+b}{c-2a}$的值是（ ）
| A． | 2 | B． | 3 | C． | -2 | D． | -3 |