题目内容
2．
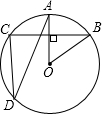如图，⊙O中，OA⊥BC，∠CDA=20°，则∠AOB的度数是40度．
分析 首先根据垂径定理得出$\widehat{AC}$=$\widehat{AB}$．再根据圆周角定理，得∠AOB=2∠CDA=40°．
解答 解：∵OA⊥BC，
∴$\widehat{AC}$=$\widehat{AB}$，
∴由圆周角定理，得∠AOB=2∠CDA=40°．
故答案为：40．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
12．对于任意有理数a，b，现用★定义一种运算：a★b=a2-b2．根据这个定义，代数式（x+y）★y可以化简为（ ）
| A． | xy+x2 | B． | xy-y2 | C． | x2+2xy | D． | x2 |
10．把直线l：y=-2x+2沿y轴正方向向上平移2个单位得到直线l′，则直线l′的解析式为（ ）
| A． | y=2x+4 | B． | y=-2x-2 | C． | y=2x-4 | D． | y=-2x+4 |
14．
如图，BD∥CE，∠1=85°，∠2=37°，则∠A的度数是（ ）
如图，BD∥CE，∠1=85°，∠2=37°，则∠A的度数是（ ）| A． | 15度 | B． | 37度 | C． | 48度 | D． | 53度 |
如图，?ABCD各顶点的坐标是：A（1，2），B（a，b），C（6，3），D（c，d），则a+b+c+d=12．