题目内容
12. 如图,?ABCD各顶点的坐标是:A(1,2),B(a,b),C(6,3),D(c,d),则a+b+c+d=12.
如图,?ABCD各顶点的坐标是:A(1,2),B(a,b),C(6,3),D(c,d),则a+b+c+d=12.
分析 如图,连接AC、BD交于点K.因为四边形ABCD是平行四边形,可知AK=KC,DK=BK,由中点坐标公式可得$\frac{a+c}{2}$=$\frac{1+6}{2}$,$\frac{b+d}{2}$=$\frac{2+3}{2}$,求出a+c,b+d即可解决问题.
解答 解:如图,连接AC、BD交于点K.
∵四边形ABCD是平行四边形,
∴AK=KC,DK=BK,
∴$\frac{a+c}{2}$=$\frac{1+6}{2}$,$\frac{b+d}{2}$=$\frac{2+3}{2}$,
∴a+c=7,b+d=5,
∴a+b+c+d=12,
故答案为12.
点评 本题考查平行四边形的性质、坐标与图形性质、中点坐标公式等知识,解题的关键是学会利用中点坐标公式解决问题,属于中考常考题型.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
20.已知点(-2,y1),(-1,y2),(1,y3)都在反比例函数y=$\frac{k}{x}$(k<0)的图象上,那么y1,y2与y3的大小关系是( )
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
7.国家将建设世界最长跨径的斜拉式大桥,计划总投资64.5亿元,用科学记数法表示为( )
| A. | 6.45×107 | B. | 64.5×108 | C. | 6.45×108 | D. | 6.45×109 |
4.方程x2-4=0的解是( )
| A. | x=±2 | B. | x=±4 | C. | x=2 | D. | x=-2 |
1.二次函数y=ax2+bx+c,自变量x与函数y的对应值如下表:
下列说法正确的是( )
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A. | 抛物线的开口向下 | B. | 当x>-3时,y随x的增大而增大 | ||
| C. | 二次函数的最小值是-2 | D. | 抛物线的对称轴x=-$\frac{5}{2}$ |
2.用一个平面分别去截下列几何体,截面不能得到圆的是( )
| A. |  | B. |  | C. |  | D. |  |
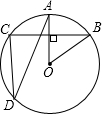 如图,⊙O中,OA⊥BC,∠CDA=20°,则∠AOB的度数是40度.
如图,⊙O中,OA⊥BC,∠CDA=20°,则∠AOB的度数是40度.