题目内容
在⊙O中，弦AB=2cm，∠ACB=30°，则⊙O的直径为考点：圆周角定理,含30度角的直角三角形
专题：
分析：连接OA，OB，先根据圆周角定理得出∠AOB=60°，故可得出△AOB是等边三角形，由此可得出结论．
解答：
解：连接OA，OB，
∵∠ACB=30°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=2cm，
∴⊙O的直径=4cm．
故答案为：4．
解：连接OA，OB，∵∠ACB=30°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=2cm，
∴⊙O的直径=4cm．
故答案为：4．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
如图，已知，PM=PN，EQ∥MN，MQ为∠PMN的平分线，且∠MQN=72°，则图中的等腰△有（ ）| A、2个 | B、3个 | C、4个 | D、5个 |
如图，已知∠BOC=2∠AOC，OD平分∠AOB，且∠COD=20°，求∠AOC的度数．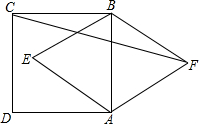
如图，正方形ABCD中，以AB为边分别在正方形内、外作等边△ABE，△ABF，则∠CFB=