题目内容
在数轴上表示不等式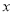 ≥-2的解集,正确的是( )
≥-2的解集,正确的是( )
A. 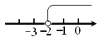 B.
B. 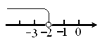 C.
C. 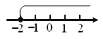 D.
D. 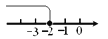
 C
【解析】试题解析:∵不等式x≥-2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥-2中是大于等于,
∴折线应向右折,
∴可排除D.
故选C.
C
【解析】试题解析:∵不等式x≥-2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥-2中是大于等于,
∴折线应向右折,
∴可排除D.
故选C.
 名校课堂系列答案
名校课堂系列答案某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
 【解析】
(1)设该厂生产甲种饮料x千克,则生产乙种饮料(650﹣x)千克,
根据题意得,,
由①得,x≤425,由②得,x≥200,
∴x的取值范围是200≤x≤425。
(2)设这批饮料销售总金额为y元,根据题意得,
,即y=﹣x+2600,
∵k=﹣1<0,
∴当x=200时,这批饮料销售总金额最大,为﹣200+2600=2400元。
【解析...
【解析】
(1)设该厂生产甲种饮料x千克,则生产乙种饮料(650﹣x)千克,
根据题意得,,
由①得,x≤425,由②得,x≥200,
∴x的取值范围是200≤x≤425。
(2)设这批饮料销售总金额为y元,根据题意得,
,即y=﹣x+2600,
∵k=﹣1<0,
∴当x=200时,这批饮料销售总金额最大,为﹣200+2600=2400元。
【解析... 某剧场为希望工程义演的文艺表演有60元和100元两种票价,某团体需购买140张,其中票价为100元的票数不少于票价为60元的票数的两倍,则购买这两种票最少共需要( )
A. 12120元 B. 12140元 C. 12160元 D. 12200元
 C
【解析】【解析】
设票价为60元的票数为x张,票价为100元的票数为y张.根据题意得: ,可得:x≤.
由题意可知:x,y为正整数,故x=46,y=94,
∴购买这两种票最少需要60×46+100×94=12160.
故选C.
C
【解析】【解析】
设票价为60元的票数为x张,票价为100元的票数为y张.根据题意得: ,可得:x≤.
由题意可知:x,y为正整数,故x=46,y=94,
∴购买这两种票最少需要60×46+100×94=12160.
故选C. 小于88的两位正整数,它的个位数字比十位数字大4,这样的两位数有_________个.
 5
【解析】设十位数字为x,则个位数字为x+4
依题意得10x+x+4<88
得x<
又∵x应为正整数,且大于0;并且0≤个位数字≤9,因而5≤x+4≤9
∴1≤x≤5,故这样的两位数有5个.
故答案:5.
5
【解析】设十位数字为x,则个位数字为x+4
依题意得10x+x+4<88
得x<
又∵x应为正整数,且大于0;并且0≤个位数字≤9,因而5≤x+4≤9
∴1≤x≤5,故这样的两位数有5个.
故答案:5. 下列图形中,能表示不等式组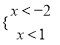 解集的是( )
解集的是( )
A.  B.
B. 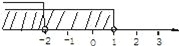
C. 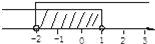 D.
D. 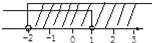
 A
【解析】如果是表示大于或小于号的点要用空心,
如果是表示大于等于或小于等于号的点用实心.
故选A.
A
【解析】如果是表示大于或小于号的点要用空心,
如果是表示大于等于或小于等于号的点用实心.
故选A. 如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
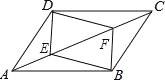
 详见解析.
【解析】
试题分析:(1)根据全等三角形的判定方法,判断出△ADE≌△CBF,即可推得DE=BF.(2)首先判断出DE∥BF;然后根据一组对边平行且相等的四边形是平行四边形,推得四边形DEBF是平行四边形即可.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△AD...
详见解析.
【解析】
试题分析:(1)根据全等三角形的判定方法,判断出△ADE≌△CBF,即可推得DE=BF.(2)首先判断出DE∥BF;然后根据一组对边平行且相等的四边形是平行四边形,推得四边形DEBF是平行四边形即可.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△AD... 如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于 cm.
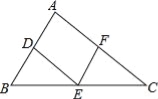
 14.
【解析】
试题分析:∵D、E分别AB、BC的中点,∴AD=AB,DE=AC.同理AF=AC,EF=AB.∴l四边形ADEF=AD+DE+EF+AF=(AB+AC+AB+AC)=AB+AC=14cm.
14.
【解析】
试题分析:∵D、E分别AB、BC的中点,∴AD=AB,DE=AC.同理AF=AC,EF=AB.∴l四边形ADEF=AD+DE+EF+AF=(AB+AC+AB+AC)=AB+AC=14cm. 在下列条件中,能够判定一个四边形是平行四边形的是( )
A. 一组对边平行,另一组对边相等
B. 一组对边相等,一组对角相等
C. 一组对边平行,一条对角线平分另一条对角线
D. 一组对边相等,一条对角线平分另一条对角线
 C
【解析】A、错误.这个四边形有可能是等腰梯形.
B、错误.不满足三角形全等的条件,无法证明相等的一组对边平行.
C、正确.可以利用三角形全等证明平行的一组对边相等.故是平行四边形.
D、错误.不满足三角形全等的条件,无法证明相等的一组对边平行.
故选C.
C
【解析】A、错误.这个四边形有可能是等腰梯形.
B、错误.不满足三角形全等的条件,无法证明相等的一组对边平行.
C、正确.可以利用三角形全等证明平行的一组对边相等.故是平行四边形.
D、错误.不满足三角形全等的条件,无法证明相等的一组对边平行.
故选C. 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
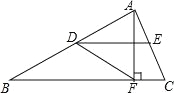
A.4 B.8 C.2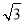 D.4
D.4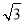
 D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D.
D.
【解析】
试题分析:在RT△ABF中,∠AFB=90°,AD=DB,DF=4,利用直角三角形斜边中线性质可得AB=2DF=8,再由AD=DB,AE=EC,可得DE∥BC,∠ADE=∠ABF=30°,所以AF=AB=4,由勾股定理可得BF=4.故选D. 
