��Ŀ����
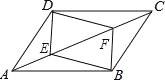
��ͼ����?ABCD�У���E��F�ڶԽ���AC�ϣ���AE=CF����֤��
��1��DE=BF��
��2���ı���DEBF��ƽ���ı��Σ�
 �������.
��������
�����������1������ȫ�������ε��ж��������жϳ���ADE�ա�CBF�������Ƶ�DE=BF����2�������жϳ�DE��BF��Ȼ�����һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��Ƶ��ı���DEBF��ƽ���ı��μ��ɣ�
�����������1�����ı���ABCD��ƽ���ı��Σ�
��AD��CB��AD=CB��
���DAE=��BCF��
�ڡ�ADE�͡�CBF�У�
���AD...
�������.
��������
�����������1������ȫ�������ε��ж��������жϳ���ADE�ա�CBF�������Ƶ�DE=BF����2�������жϳ�DE��BF��Ȼ�����һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ��Ƶ��ı���DEBF��ƽ���ı��μ��ɣ�
�����������1�����ı���ABCD��ƽ���ı��Σ�
��AD��CB��AD=CB��
���DAE=��BCF��
�ڡ�ADE�͡�CBF�У�
���AD...
һ�����Σ����߳��ֱ�Ϊxcm��10cm����������ܳ�С��80cm���������100cm2����x��ȡֵ��Χ��__��
 10��x��30
����������������
���ε��ܳ���2��x+10��cm�������10xcm2���������⣬�ã�
��
�ⲻ��ʽ��2��x+10����80��
��ã�x��30��
�ⲻ��ʽ��10x��100��
��ã�x��10��
����x��ȡֵ��Χ�ǣ�10��x��30��
�ʴ�Ϊ��10��x��30��
10��x��30
����������������
���ε��ܳ���2��x+10��cm�������10xcm2���������⣬�ã�
��
�ⲻ��ʽ��2��x+10����80��
��ã�x��30��
�ⲻ��ʽ��10x��100��
��ã�x��10��
����x��ȡֵ��Χ�ǣ�10��x��30��
�ʴ�Ϊ��10��x��30�� �ס���ԭ�д��800Ԫ��1800Ԫ���ӱ��¿�ʼ����ÿ�´�400Ԫ����ÿ�´�200Ԫ����������˴��ʱ��Ϊx�£��״�����y1Ԫ���Ҵ�����y2Ԫ��
��1����д��y1��x��y2��x֮��ĺ�����ϵʽ��
��2�����ڼ�����ʱ���״����ܳ����Ҵ��
 �������
��������
�����������1�����ݴ����=ԭ�д��+�ִ����Ǯ������ʽ���ɣ�
��2���г�һԪһ�β���ʽ��Ȼ����⼴�ɣ�
��������
��1���������⣬�ף�y1=400x+800��
�ң�y2=200x+1800��
��2���������⣬400x+800��200x+1800��
���x��5��
���ԣ��ӵ�6���¿�ʼ���״����ܳ����Ҵ��
�������
��������
�����������1�����ݴ����=ԭ�д��+�ִ����Ǯ������ʽ���ɣ�
��2���г�һԪһ�β���ʽ��Ȼ����⼴�ɣ�
��������
��1���������⣬�ף�y1=400x+800��
�ң�y2=200x+1800��
��2���������⣬400x+800��200x+1800��
���x��5��
���ԣ��ӵ�6���¿�ʼ���״����ܳ����Ҵ�� ����ʽ�� ����С������Ϊ��������
����С������Ϊ��������
A. ��1 B. 0 C. 1 D. 4
 B
����������3x��4��8���ã�x��4��
��ʽ��Ľ⼯�ǣ�����x��4��
����С���������ǣ�0��
��ѡB��
B
����������3x��4��8���ã�x��4��
��ʽ��Ľ⼯�ǣ�����x��4��
����С���������ǣ�0��
��ѡB�� �������ϱ�ʾ����ʽ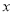 �ݣ�2�Ľ⼯����ȷ���ǣ� ��
�ݣ�2�Ľ⼯����ȷ���ǣ� ��
A. 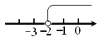 B.
B. 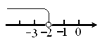 C.
C. 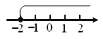 D.
D. 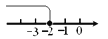
 C
������������������߲���ʽx��-2�а������ںţ�
�������ʵ��Բ�㣬
����ų�A��B��
�߲���ʽx��-2���Ǵ��ڵ��ڣ�
������Ӧ�����ۣ�
����ų�D��
��ѡC��
C
������������������߲���ʽx��-2�а������ںţ�
�������ʵ��Բ�㣬
����ų�A��B��
�߲���ʽx��-2���Ǵ��ڵ��ڣ�
������Ӧ�����ۣ�
����ų�D��
��ѡC�� ��ͼ����?ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��
��1����֤��AB=CF��
��2������DE����AD=2AB����֤��DE��AF��
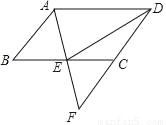
 ��1��֤����������2��֤��������
�������������������1������?ABCD�У�E��BC���е㣬����ASA�������ж���ABE�ա�FCE���̶�֤�ý��ۣ���2����AD=2AB��AB=FC=CD���ɵ�AD=DF�����ɡ�ABE�ա�FCE���ɵ�AE=EF��Ȼ���������ߺ�һ��֤�ý��ۣ�
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB��DF�� ���ABE=��FCE�� ��EΪBC�е㣬 ��BE=C...
��1��֤����������2��֤��������
�������������������1������?ABCD�У�E��BC���е㣬����ASA�������ж���ABE�ա�FCE���̶�֤�ý��ۣ���2����AD=2AB��AB=FC=CD���ɵ�AD=DF�����ɡ�ABE�ա�FCE���ɵ�AE=EF��Ȼ���������ߺ�һ��֤�ý��ۣ�
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB��DF�� ���ABE=��FCE�� ��EΪBC�е㣬 ��BE=C... һ������ε��ڽǺ�����Ǻ͵�2�������������εı���Ϊ______��
 6
���������߶���ε���Ǻ���360�ȣ�����ε��ڽǺ�����Ǻ͵�2����
���ڽǺ���720�ȣ�
720��180+2=6��
������������������
�ʴ�Ϊ��6��
6
���������߶���ε���Ǻ���360�ȣ�����ε��ڽǺ�����Ǻ͵�2����
���ڽǺ���720�ȣ�
720��180+2=6��
������������������
�ʴ�Ϊ��6�� ��ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��F�ֱ���OA��OC��
��1������������������OB=OD���ڡ�1=��2����OE=OF���������ѡȡ��������֤����BEO�ա�DFO��
��2���ڣ�1������������ѡ������ǰ���£�����AE=CF����֤���ı���ABCD��ƽ���ı��Σ�
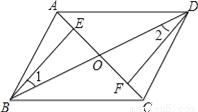
 ��1������������2��������.
�������������������1��ѡȡ�٢ڣ�����ASA�ж���BEO�ա�DFO��Ҳ��ѡȡ�ڢۣ�����AAS�ж���BEO�ա�DFO������ѡȡ�٢ۣ�����SAS�ж���BEO�ա�DFO��
��2�����ݡ�BEO�ա�DFO�ɵ�EO��FO��BO��DO���ٸ��ݵ�ʽ�����ʿɵ�AO��CO�����������Խ�����ƽ�ֵ��ı�����ƽ���ı��οɵý��ۣ�
���������
֤������1��ѡȡ�٢ڣ�
...
��1������������2��������.
�������������������1��ѡȡ�٢ڣ�����ASA�ж���BEO�ա�DFO��Ҳ��ѡȡ�ڢۣ�����AAS�ж���BEO�ա�DFO������ѡȡ�٢ۣ�����SAS�ж���BEO�ա�DFO��
��2�����ݡ�BEO�ա�DFO�ɵ�EO��FO��BO��DO���ٸ��ݵ�ʽ�����ʿɵ�AO��CO�����������Խ�����ƽ�ֵ��ı�����ƽ���ı��οɵý��ۣ�
���������
֤������1��ѡȡ�٢ڣ�
... ��ͼ��ƽ���ı���ABCD���ܳ���26cm���Խ���AC��BD���ڵ�O��AC��AB��E��BC�е㣬��AOD���ܳ��ȡ�AOB���ܳ���3cm����AE�ij���Ϊ��������
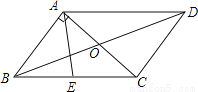
A. 3cm B. 4cm C. 5cm D. 8cm
 B
�������������������?ABCD���ܳ�Ϊ26cm��
��AB+AD=13cm��OB=OD��
�ߡ�AOD���ܳ��ȡ�AOB���ܳ���3cm��
�ࣨOA+OD+AD��-��OA+OB+AB��=AD-AB=3cm��
��AB=5cm��AD=8cm��
��BC=AD=8cm��
��AC��AB��E��BC�е㣬
��AE=BC=4cm.
��ѡB��
B
�������������������?ABCD���ܳ�Ϊ26cm��
��AB+AD=13cm��OB=OD��
�ߡ�AOD���ܳ��ȡ�AOB���ܳ���3cm��
�ࣨOA+OD+AD��-��OA+OB+AB��=AD-AB=3cm��
��AB=5cm��AD=8cm��
��BC=AD=8cm��
��AC��AB��E��BC�е㣬
��AE=BC=4cm.
��ѡB�� 
