题目内容
某饮料厂以300千克的A种果汁和240千克的B种果汁为原料,配制生产甲、乙两种新型饮料,已知每千克甲种饮料含0.6千克A种果汁,含0.3千克B种果汁;每千克乙种饮料含0.2千克A种果汁,含0.4千克B种果汁.饮料厂计划生产甲、乙两种新型饮料共650千克,设该厂生产甲种饮料x(千克).
(1)列出满足题意的关于x的不等式组,并求出x的取值范围;
(2)已知该饮料厂的甲种饮料销售价是每1千克3元,乙种饮料销售价是每1千克4元,那么该饮料厂生产甲、乙两种饮料各多少千克,才能使得这批饮料销售总金额最大?
 【解析】
(1)设该厂生产甲种饮料x千克,则生产乙种饮料(650﹣x)千克,
根据题意得,,
由①得,x≤425,由②得,x≥200,
∴x的取值范围是200≤x≤425。
(2)设这批饮料销售总金额为y元,根据题意得,
,即y=﹣x+2600,
∵k=﹣1<0,
∴当x=200时,这批饮料销售总金额最大,为﹣200+2600=2400元。
【解析...
【解析】
(1)设该厂生产甲种饮料x千克,则生产乙种饮料(650﹣x)千克,
根据题意得,,
由①得,x≤425,由②得,x≥200,
∴x的取值范围是200≤x≤425。
(2)设这批饮料销售总金额为y元,根据题意得,
,即y=﹣x+2600,
∵k=﹣1<0,
∴当x=200时,这批饮料销售总金额最大,为﹣200+2600=2400元。
【解析...
练习册系列答案
相关题目
能判定四边形ABCD为平行四边形的是( ).
A. AB∥CD,AD=BC
B. ∠A=∠B,∠C=∠D
C. AB=CD,AD=BC
D. AB=AD,CB=CD
 C
【解析】选项C中,两组对边分别相等的四边形是平行四边形.
C
【解析】选项C中,两组对边分别相等的四边形是平行四边形. 下列变形错误的是( )
A. 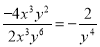 B.
B. 
C.  D.
D. 
 D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D.
D
【解析】试题解析:A选项分子和分母同时除以最大公因式;B选项的分子和分母互为相反数;C选项分子和分母同时除以最大公因式,D选项正确的变形是所以答案是D选项
故选D. 把分式 中的m和n都扩大4倍,那么分式的值( )
中的m和n都扩大4倍,那么分式的值( )
A. 也扩大4倍 B. 扩大为原来的4倍 C. 不变 D. 缩小为原来的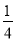
 C
【解析】试题分析:把分式中的m、n分别用4m、4n代替,
得==,
所以分式的值不变,
故选C.
C
【解析】试题分析:把分式中的m、n分别用4m、4n代替,
得==,
所以分式的值不变,
故选C. 计算 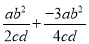 的结果是( )
的结果是( )
A.  B.
B.  C.
C.  D. -
D. -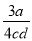
 C
【解析】试题分析:原式=+
=
=.
故选C.
C
【解析】试题分析:原式=+
=
=.
故选C. 一个矩形,两边长分别为xcm和10cm,如果它的周长小于80cm,面积大于100cm2,则x的取值范围是__.
 10<x<30
【解析】【解析】
矩形的周长是2(x+10)cm,面积是10xcm2.根据题意,得:
,
解不等式:2(x+10)<80,
解得:x<30,
解不等式:10x>100,
解得:x>10,
所以x的取值范围是:10<x<30.
故答案为:10<x<30.
10<x<30
【解析】【解析】
矩形的周长是2(x+10)cm,面积是10xcm2.根据题意,得:
,
解不等式:2(x+10)<80,
解得:x<30,
解不等式:10x>100,
解得:x>10,
所以x的取值范围是:10<x<30.
故答案为:10<x<30. x取什么值时,代数式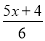 的值不小于
的值不小于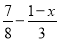 的值?并求x的最小值.
的值?并求x的最小值.
 x≥-,最小值为-.
【解析】【试题分析】根据题意,列出不等式 ,求出不等式的解集x≥-即可.
【试题解析】
由题意得:
,
去分母得: ,
去括号得:
移项得:
合并同类项得: 系数化为1得: .
x的最小值为-.
故答案为x≥-,最小值为-.
x≥-,最小值为-.
【解析】【试题分析】根据题意,列出不等式 ,求出不等式的解集x≥-即可.
【试题解析】
由题意得:
,
去分母得: ,
去括号得:
移项得:
合并同类项得: 系数化为1得: .
x的最小值为-.
故答案为x≥-,最小值为-. 如图,已知AB∥CD,AE=CF,则下列条件中不一定能使△ABE≌△CDF的是( )

A. AB=CD B. BE∥DF C. ∠B=∠D D. BE=DF
 D
【解析】∵AB∥CD,
∴∠A=∠C,
又∵AE=CF,
∴(1)添加“AB=CD”,可由“SAS”判定△ABE≌△CDF;
(2)添加“BE∥DF”可得∠FEB=∠EFD,进一步可得∠AEB=∠CFD,从而可由“ASA”判定△ABE≌△CDF;
(3)添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF;
(4)添加“BE=DF”不能判定△ABE≌...
D
【解析】∵AB∥CD,
∴∠A=∠C,
又∵AE=CF,
∴(1)添加“AB=CD”,可由“SAS”判定△ABE≌△CDF;
(2)添加“BE∥DF”可得∠FEB=∠EFD,进一步可得∠AEB=∠CFD,从而可由“ASA”判定△ABE≌△CDF;
(3)添加“∠B=∠D”可由“AAS”判定△ABE≌△CDF;
(4)添加“BE=DF”不能判定△ABE≌... 在数轴上表示不等式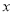 ≥-2的解集,正确的是( )
≥-2的解集,正确的是( )
A. 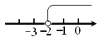 B.
B. 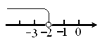 C.
C. 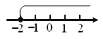 D.
D. 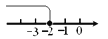
 C
【解析】试题解析:∵不等式x≥-2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥-2中是大于等于,
∴折线应向右折,
∴可排除D.
故选C.
C
【解析】试题解析:∵不等式x≥-2中包含等于号,
∴必须用实心圆点,
∴可排除A、B,
∵不等式x≥-2中是大于等于,
∴折线应向右折,
∴可排除D.
故选C. 
