题目内容
已知抛物线y=
x2和直线y=ax+1.求证:不论a取何值,抛物线与直线必有两个不同的交点.
| 1 |
| 4 |
考点:二次函数的性质
专题:证明题
分析:联立两函数解析式消掉未知数y得到关于x的一元二次方程,再利用根的判别式证明即可.
解答:证明:联立
消掉y得,
x2-ax-1=0,
∵△=(-a)2-4×
×(-1)=a2+1>0,
∴不论a取何值,方程一定有两个实数根,
∴不论a取何值,抛物线与直线必有两个不同的交点.
|
| 1 |
| 4 |
∵△=(-a)2-4×
| 1 |
| 4 |
∴不论a取何值,方程一定有两个实数根,
∴不论a取何值,抛物线与直线必有两个不同的交点.
点评:本题考查了二次函数的性质,根的判别式的应用,求出△>0是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
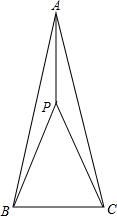 在△ABC中,AB=AC,∠BAC=30°,点P为△ABC内一点,PA=2,PB=
在△ABC中,AB=AC,∠BAC=30°,点P为△ABC内一点,PA=2,PB=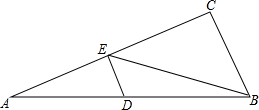 如图,在Rt△ABC中,∠C=90°,DE⊥AC于E,点D在线段AB上,已知AE=12,AD=13,CE=15,则AB=
如图,在Rt△ABC中,∠C=90°,DE⊥AC于E,点D在线段AB上,已知AE=12,AD=13,CE=15,则AB=