题目内容
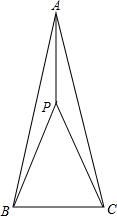 在△ABC中,AB=AC,∠BAC=30°,点P为△ABC内一点,PA=2,PB=
在△ABC中,AB=AC,∠BAC=30°,点P为△ABC内一点,PA=2,PB=| 5 |
| 3 |
考点:旋转的性质,等腰三角形的性质,勾股定理的逆定理
专题:计算题
分析:由于AB=AC,∠BAC=30°,根据旋转的定义可把△ABP绕点A逆时针旋转30°得到△ACD,作PH⊥AD于D,如图,则根据旋转的性质AD=AP=2,∠PAD=30°,CD=BP=
,∠ADC=∠APB,则根据等腰三角形的性质和三角形内角和定理可计算出∠ADP=75°;在Rt△APD中根据含30度的直角三角形三边的关系得到PH=
AP=1,AH=
PH=
,则HD=AD-AH=2-
,再在Rt△PDH中,根据勾股定理计算出PD2=8-4
,而在△CPD中由于PD2+CD2=PC2,则根据勾股定理的逆定理得到△PCD为直角三角形,∠PDC=90°,所以∠ADC=∠ADP+∠PDC=165°,于是有∠APB=165°.
| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
解答: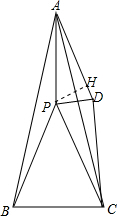 解:∵AB=AC,∠BAC=30°,
解:∵AB=AC,∠BAC=30°,
∴将△ABP绕点A逆时针旋转30°得到△ACD,作PH⊥AD于D,如图,
∴AD=AP=2,∠PAD=30°,CD=BP=
,∠ADC=∠APB,
∴∠ADP=
(180°-30°)=75°,
在Rt△APD中,PH=
AP=1,AH=
PH=
,
∴HD=AD-AH=2-
,
在Rt△PDH中,PD2=PH2+HD2=12+(2-
)2=8-4
,
在△CPD中,∵PD2=8-4
,CD2=(
)2=5,PC2=(2
-1)2=13-4
,
∴PD2+CD2=PC2,
∴△PCD为直角三角形,∠PDC=90°,
∴∠ADC=∠ADP+∠PDC=165°,
∴∠APB=165°.
 解:∵AB=AC,∠BAC=30°,
解:∵AB=AC,∠BAC=30°,∴将△ABP绕点A逆时针旋转30°得到△ACD,作PH⊥AD于D,如图,
∴AD=AP=2,∠PAD=30°,CD=BP=
| 5 |
∴∠ADP=
| 1 |
| 2 |
在Rt△APD中,PH=
| 1 |
| 2 |
| 3 |
| 3 |
∴HD=AD-AH=2-
| 3 |
在Rt△PDH中,PD2=PH2+HD2=12+(2-
| 3 |
| 3 |
在△CPD中,∵PD2=8-4
| 3 |
| 5 |
| 3 |
| 3 |
∴PD2+CD2=PC2,
∴△PCD为直角三角形,∠PDC=90°,
∴∠ADC=∠ADP+∠PDC=165°,
∴∠APB=165°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和勾股定理的逆定理.

练习册系列答案
相关题目
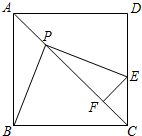 已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.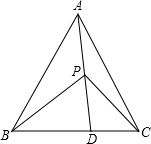 如图所示,在△ABC中,AB=AC,BD=2DC,P在AD上,∠BAC=∠BPD,求证:∠BPD=2∠CPD.
如图所示,在△ABC中,AB=AC,BD=2DC,P在AD上,∠BAC=∠BPD,求证:∠BPD=2∠CPD.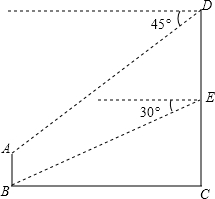 在小明和小刚家的楼前有一盏路灯AB,高为4m,小明家在3楼的E处,他站在窗口看B处的俯角为30°.小刚家在D处,他站在窗口看A处的俯角为45°,路灯与楼的距离为20m.你能知道小刚家大约是几楼吗?
在小明和小刚家的楼前有一盏路灯AB,高为4m,小明家在3楼的E处,他站在窗口看B处的俯角为30°.小刚家在D处,他站在窗口看A处的俯角为45°,路灯与楼的距离为20m.你能知道小刚家大约是几楼吗?