题目内容
2. 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=$\frac{2}{x}$于点D,从点D分别作两坐标轴的垂线DC、OE,垂足分别为C、E,连接BC、OD.
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,交双曲线y=$\frac{2}{x}$于点D,从点D分别作两坐标轴的垂线DC、OE,垂足分别为C、E,连接BC、OD.(1)请找出一个等腰三角形;
(2)当b=-1时,求出点D坐标并判断四边形OBCD的形状;
(3)当b为任意实数时(b≠0),求证:AD•BD是定值.
分析 (1)根据直线的k值等于1,与坐标轴相交所成的锐角是45°,所以与坐标轴所成夹角为锐角的直角三角形都是等腰直角三角形;
(2)根据题意列出方程组求出点D的坐标,得到DC=1,根据直线与坐标轴的交点的求法求出OB,根据平行四边形的判定定理证明;
(3)根据等腰直角三角形斜边等于直角边的$\sqrt{2}$倍,用CD表示出AD的长度,用DE表示出BD的长度,再根据反比例函数解析式,CD•DE的值等于k值进行解答;
解答  解:(1)∵直线y=x+b,
解:(1)∵直线y=x+b,
∴比例系数k=1,
∴∠EBD=∠DAC=45°,
又DC⊥x轴,DE⊥y轴,
∴△AOB、△ACD、△BDE是等腰直角三角形;
(2)由题意得,$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{2}{x}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=1}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-1}\\{{y}_{2}=-2}\end{array}\right.$,
∵点D在第一象限,
∴点D的坐标为(2,1),
∴DC=1,
∵直线y=x-1与y轴的交点坐标为(0,-1),
∴OB=1,
∴DC=OB,又DC∥OB,
∴四边形OBCD是平行四边形;
(3)证明:由(1)知△ACD和△BDE均为等腰直角三角形.
∴AD=$\sqrt{2}$CD,BD=$\sqrt{2}$DE.
∵点D在双曲线y=$\frac{2}{x}$上,
∴CD•DE=2,
∴AD•BD=$\sqrt{2}$CD•$\sqrt{2}$DE=2×2=4,4为定值.
点评 本题考查的是反比例函数知识的综合运用,掌握一次函数与反比例函数的交点的求法、角平分线的判定、等腰直角三角形的性质以及平行四边形的判定定理是解题的关键.

| A. | x≠0 | B. | x≠-3 | C. | x≠3 | D. | x≠3且x≠0 |
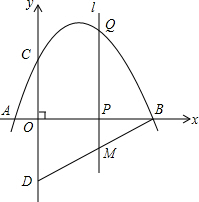 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、点B,与y轴交于点C、点D与点C关于x轴对称,点P是x轴上一动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、点B,与y轴交于点C、点D与点C关于x轴对称,点P是x轴上一动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q. 如图,B在线段AC上,且BC=2AB,D,E分别是AB,BC的中点.则下列结论:①AB=$\frac{1}{3}$AC;②B是AE的中点;③EC=2BD;④DE=AB.其中正确的有( )
如图,B在线段AC上,且BC=2AB,D,E分别是AB,BC的中点.则下列结论:①AB=$\frac{1}{3}$AC;②B是AE的中点;③EC=2BD;④DE=AB.其中正确的有( )