��Ŀ����
12��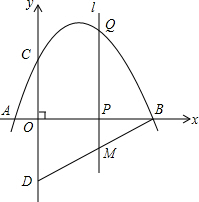 ��ͼ��������y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x����һ���㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��ͼ��������y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x����һ���㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q����1����ֱ��BD�Ľ���ʽ��
��2������P���߶�OB���˶�ʱ��ֱ��l��BD�ڵ�M����̽��mΪ��ֵʱ�ı���CQMD��ƽ���ı��Σ�
��3����P���˶������У��Ƿ���ڵ�Q��ʹ��BDQ����BDΪֱ�DZߵ�ֱ�������Σ������ڣ������Q���ꣻ�������ڣ�˵�����ɣ�
���� ��1���������C�����꣬�ٸ��ݶԳƿ����D�����꣬�ٽ�������߽��������B�����꣬���ô���ϵ���������ֱ��BD����ʽ��
��2����P������ɷֱ��ʾ��M��Q�����꣬����ƽ���ı��ε����ʿɵõ�����m�ķ��̣������m��ֵ��
��3���ɣ�2���е�Q�����꣬���ù��ɶ����ɷֱ��ʾ��BQ��BD��DQ��������ֱ�������ε��ж��ɵõ�����m�ķ��̣�����õ�Q�����꣮
��� �⣺
��1����y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2�У���x=0�ɵ�y=2��
��C��0��2����
��C��D����x��Գƣ�
��D��0��-2����
��y=0�ɵ�-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0�����x1=-1��x2=4��
��B��4��0����
��BD����ʽΪy=kx+b����$\left\{\begin{array}{l}{b=-2}\\{4k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-2}\end{array}\right.$��
��ֱ��BD����ʽΪy=$\frac{1}{2}$x-2��
��2����P��m��0����
��M��m��$\frac{1}{2}$m-2����Q��m��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2����
��CQMD��ƽ���ı��Σ�
��QM��CD��
��QM=CD=4��
����P��OB���˶�ʱQM=-$\frac{1}{2}$m2+$\frac{3}{2}$m+2-��$\frac{1}{2}$m-2��=-$\frac{1}{2}$m2+m+4=4��
���m1=0����ȥ����m2=2��
�൱m=2ʱ���ı���CQMDΪƽ���ı��Σ�
��3���ɣ�2����֪Q��m��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2������B��4��0����D��0��-2����
��BQ2=��m-4��2+��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2��2��DQ2=m2+[��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2��+2]2��BD2=20��
�ٵ��Ե�BΪֱ�Ƕ���ʱ������DQ2=BQ2+BD2��
��m2+[��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2��+2]2=��m-4��2+��-$\frac{1}{2}$m2+$\frac{3}{2}$m+2��2+20�����m1=3��m2=4��
���Q����Ϊ��4��0�����ᣩ��3��2����
�ڵ���DΪֱ�Ƕ���ʱ��ͬ������m3=-1��m4=8��
���Q������-1��0����8��-18����
���Ͽ�֪�������������ĵ�Q��������Ϊ��3��2����-1��0����8��-18����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ������ƽ���ı��ε����ʡ����ɶ���������˼�뼰��������˼���֪ʶ�㣮�ڣ�1�������B��D�����ǽ���Ĺؼ����ڣ�2������m��ʾ��QM�ij��ǽ���Ĺؼ����ڣ�3������m�ֱ��ʾ��BQ��DQ�ij��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�

 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
 ��ͼ����ABC�ڽ��ڡ�O��AB��ֱ������O������PC��BA���ӳ����ڵ�P��OF��BC��AC�ڵ�E����PC�ڵ�F������AF��
��ͼ����ABC�ڽ��ڡ�O��AB��ֱ������O������PC��BA���ӳ����ڵ�P��OF��BC��AC�ڵ�E����PC�ڵ�F������AF�� ��ͼ�����κ���y=ax2+bx-3��ͼ����x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C���������ߵĶ���ΪM��
��ͼ�����κ���y=ax2+bx-3��ͼ����x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C���������ߵĶ���ΪM�� ��ͼ��ֱ��y=x+b��b��0������������A��B���㣬��˫����y=$\frac{2}{x}$�ڵ�D���ӵ�D�ֱ�����������Ĵ���DC��OE������ֱ�ΪC��E������BC��OD��
��ͼ��ֱ��y=x+b��b��0������������A��B���㣬��˫����y=$\frac{2}{x}$�ڵ�D���ӵ�D�ֱ�����������Ĵ���DC��OE������ֱ�ΪC��E������BC��OD��