题目内容
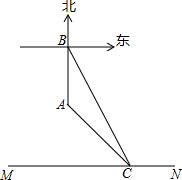如图，某数学星期小组为了测量一东西走向的小河的宽度，设计了如下测量方案，先在北岸A处测得南岸一目标C在其东南方向，再向正北方向走50米到达B处，又测得目标C在其南偏东30°方向，请你根据以上测量结果计算小河的宽度（结果用根号表示）．考点：解直角三角形的应用-方向角问题
专题：
分析：延长BA交MC于点D，设AD=x米得到DC=x，然后在Rt△BDC中利用
=tan∠DBC求得x的值即可．
| DC |
| BD |
解答：
解：延长BA交MC于点D，
由题意得：AB=50米，∠ABC=30°，∠DAC=45°，
设AD=x米，
则DC=x，
∵在Rt△BDC中，
=tan∠DBC，
∴
=
，
解得：x=
，
∴小河的宽度为
米．
解：延长BA交MC于点D，由题意得：AB=50米，∠ABC=30°，∠DAC=45°，
设AD=x米，
则DC=x，
∵在Rt△BDC中，
| DC |
| BD |
∴
| x |
| x+50 |
| ||
| 3 |
解得：x=
75
| ||
| 3 |
∴小河的宽度为
75
| ||
| 3 |
点评：本题考查了解直角三角形的应用-方向角问题，解题的关键是正确的构造直角三角形，难度不大．
练习册系列答案
相关题目
如图，AB为的直径，点C在⊙O上，点P是直径AB上的一点（不与AB重合）过点P作AB的垂线交BC的延长线于点Q．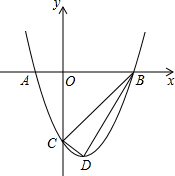
如图，已知抛物线y=ax2+bx+c 与x轴的一个交点为A（-1，0），另一个交点为B，与y轴的交点为C（0，-3），其顶点为D，对称轴为直线x=1．
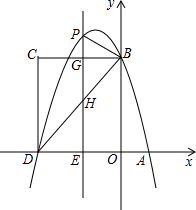如图，在平面直角坐标系中，抛物线y=-x2+bx+c与x轴交于A、D两点，与y轴交于点B，四边形OBCD是正方形．点B坐标为（0，4），已知点E（m，0）是线段DO上的动点（m＜0），过点E作PE⊥x轴交抛物线于点P，交BC于点G，交BD于点H．