题目内容
10.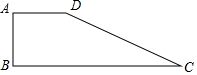 如图:四边形ABCD中,AB=4,BC=13,CD=12,AD=3,∠A=90°,求四边形ABCD的面积.
如图:四边形ABCD中,AB=4,BC=13,CD=12,AD=3,∠A=90°,求四边形ABCD的面积.
分析 先根据勾股定理求出BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
解答 解:连接BD,如图所示:
∵∠A=90°,AB=4,AD=3,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=5,
在△BCD中,
BD2+CD2=25+144=169=BC2,
∴△BCD是直角三角形,
∴S四边形ABCD=$\frac{1}{2}$AB•AD+$\frac{1}{2}$BD•CD,
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12,
=36.
答:四边形ABCD的面积是36.
点评 本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.在△ABC中,若a=2,b=3,c=4,则△ABC是( )三角形.
| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 无法确定 |
2.△ABC中,AB=13,BC=10,BC边上中线AP=12,则AB,AC关系为( )
| A. | AB>AC | B. | AB=AC | C. | AB<AC | D. | 无法确定 |
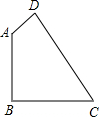 如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.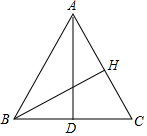 如图,AD是△ABC的中线,AD=12,AB=13,BC=10,
如图,AD是△ABC的中线,AD=12,AB=13,BC=10, 如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.
如图,已知:△ABC中,AB=AC,M、D、E分别是BC、AB、AC的中点.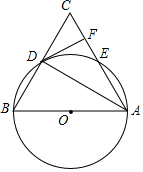 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.
如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,且BD=CD,过D作DF⊥AC,垂足为F.