题目内容
12.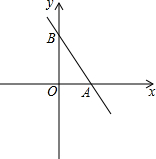 如图,一次函数y=-2x+2的直线与x轴、y轴分别交于A、B两点.
如图,一次函数y=-2x+2的直线与x轴、y轴分别交于A、B两点.(1)求出A、B两点的坐标;
(2)将直线AB向右平移2个单位长度,求平移后直线的函数关系式;
(3)写出平移过程中,直线AB在第一象限扫过的面积(不写过程).
分析 (1)分别令x=0、y=0,求出对于的y、x值,即可得出点A、B的坐标;
(2)根据平移的性质“左加右减”,将x换成x-2整理后即可得出结论;
(3)根据三角形的面积公式直接求出扫过的面积即可得出结论.
解答 解:(1)令y=-2x+2中x=0,则y=2,
∴点B(0,2);
令y=-2x+2中y=0,则0=-2x+2,解得:x=1,
∴点A(1,0).
(2)根据平移的性质可知:
平移后直线的函数关系式为:y=-2(x-2)+2=-2x+6.
(3)直线y=-2x+6与x、y轴的交点坐标为(3,0)、(0,6),
∴S=$\frac{1}{2}$×3×6-$\frac{1}{2}$×1×2=8.
答:平移过程中,直线AB在第一象限扫过的面积为8.
点评 本题考查了一次函数图象与几何变换以及三角形的面积公式,解题的关键是:(1)分别代入x=0、y=0求值;(2)以及平移性质将x换成x-2;(3)套用三角形的面积公式求值.本题属于基础题,难度不大,解决该题型题目时,根据平移的性质“上加下减,左加右减”替换函数关系式中的x、y值即可.

练习册系列答案
相关题目
2.方程2x+3y=8的正整数解的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
20.方程2x+3y=15的正整数解有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
1.如果反比例函数y=$\frac{k}{x}$的图象经过点(3,-2),则k的值是( )
| A. | -6 | B. | 6 | C. | -3 | D. | 3 |
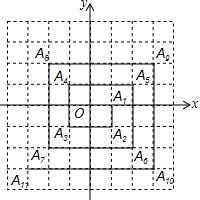 如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2017的坐标是(505,504).
如图,已知A1(1,0),A2(1,-1),A3(-1,-1),A4(-1,1),A5(2,1),…,则点A2017的坐标是(505,504). △ABC的位置如图所示:
△ABC的位置如图所示: 如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D的度数为50°.
如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D的度数为50°. 如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.