题目内容
19.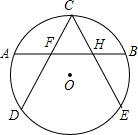 如图所示,CD,CE是⊙O的两条弦,A,B分别是$\widehat{CD}$和$\widehat{CE}$的中点,连接AB交CD于点F,交CE于点H,求证:CF=CH.
如图所示,CD,CE是⊙O的两条弦,A,B分别是$\widehat{CD}$和$\widehat{CE}$的中点,连接AB交CD于点F,交CE于点H,求证:CF=CH.
分析 利用圆周角定理,得∠CAB=∠BCE,∠CBA=∠ACD,利用三角形外角定理,得∠CFH=∠CHF,等腰三角形判定得出结论.
解答 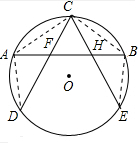 证明:连接AC,AD,BC,BE,
证明:连接AC,AD,BC,BE,
∵A是$\widehat{CD}$的中点,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠CBA=∠ACD,
∵B是$\widehat{CE}$的中点,
∴$\widehat{BC}$=$\widehat{BE}$,
∴∠CAB=∠BCE,
∵∠CFH=∠ACD+∠CAB,
∠CHF=∠BCE+∠CBA,
∴∠CFH=∠CHF,
∴CF=CH.
点评 本题主要考查了圆周角定理,三角形外角定理,等腰三角形判定定理,利用圆周角定理是解决此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.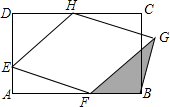 如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )
如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )
 如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )
如图,E在矩形ABCD的AD边上,AE=3,ED=5,DC=10,F,H分别在AB,CD上,四边形EFGH是菱形,则△FBG的面积S的取值范围是( )| A. | 0<S≤15 | B. | 2<S≤12 | C. | 1<S≤15 | D. | 0<S≤12 |
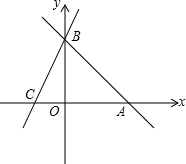 直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.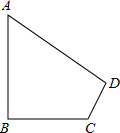 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=6,CD=4,求AB的长.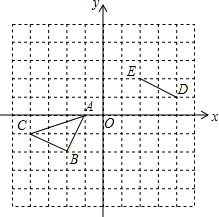 如图所示的正方形网格中,△ABC的顶点均在格点上,线段DE的两个端点也在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,线段DE的两个端点也在格点上,在所给直角坐标系中解答下列问题: 下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的主视图是( )
下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形,这个立体图形的主视图是( )


