题目内容
8. 推理填空
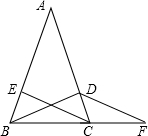
推理填空如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:CE∥DF.请完成下面的解题过程.
解:∵BD平分∠ABC,CE平分∠ACB ( 已知 )
∴∠DBC=$\frac{1}{2}$∠ABC,∠ECB=$\frac{1}{2}$∠ACB ( 角平分线的定义)
又∵∠ABC=∠ACB (已知)
∴∠DBC=∠ECB.
又∵∠DBF=∠F (已知)
∴∠F=∠ECB
∴CE∥DF同位角相等,两直线平行.
分析 结合角平分线的定义以及∠ABC=∠ACB即可得出∠DBC=∠ECB,再由∠DBF=∠F即可得出∠F=∠ECB,利用(同位角相等,两直线平行)即可得出CE∥DF.
解答 解:∵BD平分∠ABC,CE平分∠ACB ( 已知 ),
∴∠DBC=$\frac{1}{2}$∠ABC,∠ECB=$\frac{1}{2}$∠ACB( 角平分线的定义).
又∵∠ABC=∠ACB (已知),
∴∠DBC=∠ECB.
又∵∠DBF=∠F(已知),
∴∠F=∠ECB(等量代换),
∴CE∥DF(同位角相等,两直线平行).
故答案为:ABC;ACB;DBC;ECB;DBF;F;ECB;同位角相等,两直线平行.
点评 本题考查了平行线的判定以及角平分线,解题的关键是找出相等的同位角∠F=∠ECB.本题属于基础题,难度不大,解决该题型题目时,找出相等(或互补)的角是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
1.下列各组数中的互为相反数的是( )
| A. | 3与$\frac{1}{3}$ | B. | (-1)2与1 | C. | -24与 24 | D. | -(-2)与|-2| |
13.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{7}$ | C. | $\sqrt{20}$ | D. | $\sqrt{x+3}$ |
20.下列计算中正确的是( )
| A. | a×a3=a3 | B. | (a2)3=a5 | C. | (a+b)3=a3+b3 | D. | a6÷a2=a4 |
 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=3,BC=5,则S△BEF=$\frac{51}{10}$.
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=3,BC=5,则S△BEF=$\frac{51}{10}$.