题目内容
18.先化简,后求值:($\frac{a}{a+2}$+$\frac{2}{a-2}$)÷$\frac{1}{{a}^{2}-4}$,其中a=$\sqrt{3}$.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-2a+2a+4}{(a+2)(a-2)}$•(a+2)(a-2)=a2+4,
当a=$\sqrt{3}$时,原式=3+4=7.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
6.已知两个相似多边形的面积比是9:16,其中较小多边形的周长为18cm,则较大多边形的周长为( )
| A. | 24cm | B. | 27cm | C. | 28cm | D. | 32cm |
7.若直角三角形两边长分别是3和4,则第三边长为( )
| A. | 5 | B. | 6 | C. | 5或 6 | D. | 5或 $\sqrt{7}$ |
8.某汽车销售公司计划销售A、B两种型号的汽车共80辆,该公司所筹资金不少于660万元,但不超过672万元,且所筹资金全部用于购进新车,设A型汽车购进x辆,该公司销售A、B两种汽车获得利润y(万元),两种汽车的成本和售价如表:
(1)该公司对这两种汽车进货有哪几种方案?
(2)列出y关于x的函数关系式,并通过函数的性质判断如何进货该公司获得利润最大?
(3)根据市场调查,每辆B型汽车售价不会改变,每辆A型汽车的售价将会提高a万元(a>0),且所进的两种汽车可全部售出,该公司又将如何进货获得利润最大?(注:利润=售价-成本)
| A | B | |
| 成本(万元/辆) | 6 | 12 |
| 售价(万元/辆) | 9 | 16 |
(2)列出y关于x的函数关系式,并通过函数的性质判断如何进货该公司获得利润最大?
(3)根据市场调查,每辆B型汽车售价不会改变,每辆A型汽车的售价将会提高a万元(a>0),且所进的两种汽车可全部售出,该公司又将如何进货获得利润最大?(注:利润=售价-成本)
 推理填空
推理填空 2016年3月31日晚,王凯同学来到金熊国际影城看电影,进场时,发现门票还在家里,此时距离电影播放还有20分钟,于是他立即步行回家取票,同时他爸爸从家里骑自行车以王凯3倍的速度给他送票,两人在途中相遇后,爸爸立即骑自行车送王凯去金熊国际影城.如图表示的是王凯和他爸爸距离金熊国际影城的距离y(米)与时间x(分钟)之间的函数关系的图象(不完整).
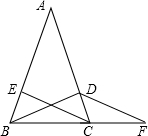
2016年3月31日晚,王凯同学来到金熊国际影城看电影,进场时,发现门票还在家里,此时距离电影播放还有20分钟,于是他立即步行回家取票,同时他爸爸从家里骑自行车以王凯3倍的速度给他送票,两人在途中相遇后,爸爸立即骑自行车送王凯去金熊国际影城.如图表示的是王凯和他爸爸距离金熊国际影城的距离y(米)与时间x(分钟)之间的函数关系的图象(不完整). 如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.
如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.