题目内容
3. 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=3,BC=5,则S△BEF=$\frac{51}{10}$.
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=3,BC=5,则S△BEF=$\frac{51}{10}$.
分析 由翻折和矩形的性质通过角的计算可得出∠C′BF=∠ABE,从而可证出△ABE≌△C′BF(ASA),进而得出AE=C′F=CF,在Rt△BAE中,利用勾股定理即可求出AE的长度,再利用分割图形求面积法即可得出S△BEF=S梯形ABFE-S△ABE,代入数据即可得出结论.
解答 解:由折叠可知:DE=BE,DC=BC′,CF=C′F,∠D=∠EBC′,∠C′=∠C.
∵四边形ABCD为矩形,
∴BA=DC=BC′,∠A=∠ABC=∠C=∠C′=90°,
∴∠C′BF+∠FBE=90°,FBE+∠ABE=90°,
∴∠C′BF=∠ABE.
在△ABE和△C′BF中,$\left\{\begin{array}{l}{∠ABE=∠C′BF}\\{BA=BC′}\\{∠A=∠C′=90°}\end{array}\right.$,
∴△ABE≌△C′BF(ASA),
∴AE=C′F=CF.
设AE=x,则BE=DE=AD-AE=5-x,
在Rt△BAE中,AB=3,∠A=90°,
∴BE2=AB2+AE2,即(5-x)2=9+x2,
解得:x=$\frac{8}{5}$.
∴AE=$\frac{8}{5}$,BF=BC-CF=$\frac{17}{5}$,
∴S△BEF=S梯形ABFE-S△ABE=$\frac{1}{2}$(AE+BF)•AB-$\frac{1}{2}$AE•AB=$\frac{51}{10}$.
故答案为:$\frac{51}{10}$.
点评 本题考查了翻折变换中折叠问题、矩形的性质、勾股定理以及全等三角形的判定与性质,解题的关键是求出AE、BF的长度.本题属于中档题,难度不大,解决该题型题目时,根据翻折变换找出相等的边角关系是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
16.下列计算中正确的是( )
| A. | m5-m2=m3 | B. | m5•m2=m7 | C. | m10÷m2=m5 | D. | (2m)5=2m5 |
11.36的平方根是( )
| A. | -6 | B. | 36 | C. | ±$\sqrt{6}$ | D. | ±6 |
 如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为16cm2.
如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2,则S△ABC的值为16cm2.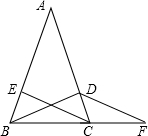 推理填空
推理填空 如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.
如图,已知DE∥BC,∠1=∠2,求证:∠B=∠C.