题目内容
20.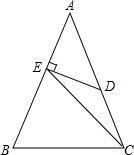 已知:如图,在△ABC中,AB=AC,∠A=45°,点D在AC上,DE⊥AB于E,且DE=DC,连结EC.请写出图中所有等腰三角形(△ABC除外),并说明理由.
已知:如图,在△ABC中,AB=AC,∠A=45°,点D在AC上,DE⊥AB于E,且DE=DC,连结EC.请写出图中所有等腰三角形(△ABC除外),并说明理由.
分析 根据等腰直角三角形的性质得到∠ADE=45°,推出∠A=∠ADE,得到△AED为等腰直角三角形,由DE=DC,得到△DEC为等腰三角形,根据∠BEC=180°-90°-22.5°67.5°,证得∠B=67.5°,得到∠B=∠BEC,得到△BEC为等腰三角形.
解答 解:等腰三角形△AED,△DEC,△BEC,
证明:∵∠A=45°,DE⊥AB于E,
∴∠AED=90°,
∴∠ADE=45°,
∴∠A=∠ADE,
∴AE=DE,
∴△AED为等腰直角三角形,
∵DE=DC,
∴△DEC为等腰三角形,
∵∠BEC=180°-90°-22.5°=67.5°,
又∵∠A=45°,AE=AC,
∴∠B=67.5°,
∴∠B=∠BEC,
∴BC=EC,
∴△BEC为等腰三角形.
点评 本题考查了等腰直角三角形的判定和性质,三角形的内角和,垂直的定义.熟练掌握等腰三角形的判定是解题的关键.

练习册系列答案
相关题目
8.在函数y=$\frac{k}{x}$(k<0)的图象上有三点Al(xl,y1)、A2(x2,y2)、A3(x3,y3),已知xl<x2<0<x3,则下列各式正确的是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y3<y1<y2 |
9.甲、乙、丙三个地方的海拔高分别是30m,-20m,-15m,那么最高的地方比最低的地方高( )
| A. | 10m | B. | 15m | C. | 50m | D. | 5m |
 如图,在△ABC中,AD是中线,BE交AD于F,且AE=EF,求证:AC=BF.
如图,在△ABC中,AD是中线,BE交AD于F,且AE=EF,求证:AC=BF. 如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=50°.
如图,直线AB和CD交于点O,∠COE=90°,OD平分∠BOF,∠BOE=50°.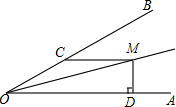 如图,OM平分∠AOB,MC∥OA,MD⊥OA于D,若∠OMD=75°,OC=8,则MD的长为( )
如图,OM平分∠AOB,MC∥OA,MD⊥OA于D,若∠OMD=75°,OC=8,则MD的长为( ) 如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的概率是$\frac{5}{7}$.
如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的概率是$\frac{5}{7}$.