题目内容
19．矩形的面积是12cm2，一边与一条对角线的比为3：5，则矩形的对角线长为5cm．分析 根据一边与一条对角线的比为3：5，求得矩形两邻边之比为3：4；根据面积求边长，最后求对角线的长．
解答 
解：如图：设AB=3x，则AC=5x，由勾股定理可知BC=4x，
矩形的面积=AB×BC=3x×4x=12，
解得x=1（舍去负值）．
所以，矩形的对角线长是5×1=5（cm）．
故答案是：5cm．
点评 本题考查了矩形的性质，解题时需要数形结合才能更直观解答，需要同学们认真作图．
练习册系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
14．$\frac{1}{27}$的立方根是（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | $±\frac{1}{3}$ | D． | 3 |
7．
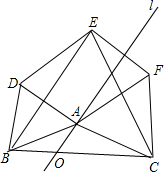如图，已知线段BC=6，O为线段BC上一点，且OB=2，过O点的直线l与BC的夹角是60°，A为l上的一个动点，分别以AC，BC为边在BC的同侧作等边△ABD，△ACF，△BCE，连接EF，则平行四边形，菱形，矩形，线段，等腰梯形中符合以点A，D，E，F构成的图形有（ ）
如图，已知线段BC=6，O为线段BC上一点，且OB=2，过O点的直线l与BC的夹角是60°，A为l上的一个动点，分别以AC，BC为边在BC的同侧作等边△ABD，△ACF，△BCE，连接EF，则平行四边形，菱形，矩形，线段，等腰梯形中符合以点A，D，E，F构成的图形有（ ）| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
如图，抛物线y=ax2+bx+1经过点（2，6），且与直线y=$\frac{1}{2}$x+1相交于A，B两点，点A在y轴上，过点B作BC⊥x轴，垂足为点C（4，0）．
5．
如图，在长方形ABCD中，CD与BC的长度比为5：12，若该长方形的周长为34，则BD的长为（ ）
如图，在长方形ABCD中，CD与BC的长度比为5：12，若该长方形的周长为34，则BD的长为（ ）| A． | 13 | B． | 12 | C． | 8 | D． | 10 |